
分析 (Ⅰ)首先对函数求导并令导数等于0,解出x的值,研究单调性,求出最值.
(Ⅱ)由 $\frac{{e}^{x}-1}{x}$-1=$\frac{{e}^{x}-x-1}{x}$,当x>0时为正,可将原不等式化为ex-(1+a)x-1<0,令g(x)=ex-(1+a)x-1,利用导数研究此函数的极值,从而得出存在正数x=ln(a+1),使原不等式成立.
(Ⅲ)主要还是借助于指数运算的知识构造出能够利用(1)的结论,变成两个函数(值)间的大小比较,从而最终化为函数的单调性问题.
解答 解:(Ⅰ)∵f′(x)=λg[λx+(1-λ)a]-λg′(x),
由f′(x)>0得,g[λx+(1-λ)a]>g′(x),
∴λx+(1-λ)a>x,即(1-λ)(x-a)<0,又因为0<λ<1,所以x<a,
故当x<a时,f′(x)>0;当x>a时,f′(x)<0;所以原函数在(-∞,a)递增,在(a,+∞)递减
∴当x=a时,f(x)取最大值f(a)=ea.
(Ⅱ)证明:∵|$\frac{{e}^{x}-1}{x}$-1|=|$\frac{{e}^{x}-x-1}{x}$|,
又当x>0时,令h(x)=ex-x-1,则h′(x)=ex-1>0,
故h(x)>h(0)=0,
因此原不等式化为 $\frac{{e}^{x}-x-1}{x}$<a,即ex-(1+a)x-1<0,
令g(x)=ex-(1+a)x-1,则g′(x)=ex-(1+a),
由g′(x)=0得:ex=(1+a),解得x=ln(a+1),
当0<x<ln(a+1)时,g′(x)<0;当x>ln(a+1)时,g′(x)>0.
故当x=ln(a+1)时,g(x)取最小值g[ln(a+1)]=a-(1+a)ln(a+1),
令s(a)=$\frac{a}{1+a}$-ln(1+a),则s′(a)=$\frac{1}{{(1+a)}^{2}}$-$\frac{1}{1+a}$=-$\frac{a}{{(1+a)}^{2}}$<0.
故s(a)<s(0)=0,即g[ln(a+1)]=a-(1+a)ln(a+1)<0.
因此,存在正数x=ln(a+1),使原不等式成立.
(Ⅲ)证明:对任意正数a1,a2,一定存在实数x1,x2使a1=ex1,a2=ex2,
则a1λ1•a2 λ2=e λ1x1•e λ2x2,λ1a1+λ2a2=λ1ex1+λ2${e}^{{x}_{2}}$,
原不等式 a1λ1•a2 λ2≤λ1a1+λ2a2?e λ1x1+λ2x2≤λ1ex1+λ2ex2,
?g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2)
由(1)f(x)≤(1-λ)g(a)
故g[λa+(1-λ)a]≤λg(x)+(1-λ)g(a)
令x=x1,a=x2,λ=λ1,1-λ=λ2
从而g(λ1x1+λ2x2)≤λ1g(x1)+λ2g(x2)
故e λ1x1+λ2x2≤λ1ex1+λ2ex2成立,
即对任意正数a1a2都有a1 λ1a2 λ2≤λ1a1+λ2a2.
原式得证.
点评 本题主要考查学生对函数的单调性与导数的关系,函数的最值与导数的关系等知识点的理解,有一定难度,属能力题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 49% | B. | 53% | C. | 61% | D. | 88% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
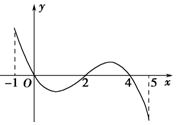 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com