
如图,菱形ABCD的边长为2,∠BAD=60º, M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
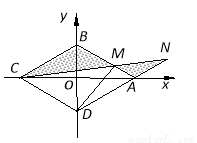
(1)试用t表示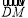 与
与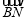 ,并求它们所成角的大小;
,并求它们所成角的大小;
(2)设f(t)=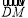 ·
·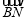 ,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数
,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数 的取值范围:
的取值范围:
①存在t1,t2∈(0,1),使得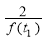 =g(t2);
=g(t2);
②对任意t1∈(0,1),恒存在t2∈(0,1),使得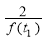 =g(t2).
=g(t2).
(1)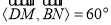 ;(2)①
;(2)①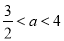 ;②
;②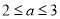 .
.
【解析】
试题分析:(1)过点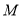 作坐标轴的垂线段,由菱形
作坐标轴的垂线段,由菱形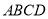 的边长为2,
的边长为2, ,
,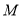 为
为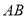 边上不与端点重合的动点,
边上不与端点重合的动点,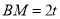 ,可得
,可得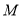 点的坐标,进而可得向量
点的坐标,进而可得向量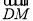 的坐标,由
的坐标,由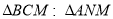 ,可得
,可得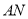 的长,进而得到
的长,进而得到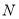 点坐标,可得向量
点坐标,可得向量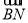 的坐标,结合向量夹角公式,可得他们的夹角;(2)由(1)可得
的坐标,结合向量夹角公式,可得他们的夹角;(2)由(1)可得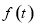 的解析式,分别求出两个函数的值域
的解析式,分别求出两个函数的值域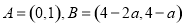 ;①若存在
;①若存在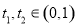 ,使得
,使得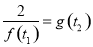 成立,则只要两函数的值域
成立,则只要两函数的值域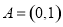 与
与 存在公共元素即可,②对任意
存在公共元素即可,②对任意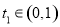 ,恒存在
,恒存在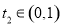 ,使得
,使得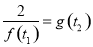 成立,则
成立,则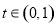 时,函数
时,函数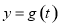 必取遍函数
必取遍函数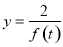 值域
值域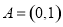 中的所有值,此即
中的所有值,此即 ,从而可得
,从而可得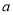 取值范围.
取值范围.
试题解析:(1) 过点M作坐标轴的垂线段,则依题设易求得
M点的坐标为:M(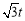 , 1-t) ⇒
, 1-t) ⇒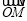 =(
=(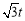 , 1-t),··· ⑴
, 1-t),··· ⑴
依题设知:△ABD为正三角形,故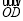 =(0, -1),由此知:
=(0, -1),由此知:
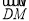 =
=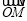 -
-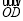 =(
=(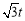 , 2-t),······ ⑵
, 2-t),······ ⑵
又依题设知:△BCM∽△ANM ⇒ 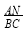 =
= =
=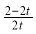 =
=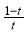 ⇒ AN=
⇒ AN=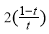 ,又∠NAx=30º,
,又∠NAx=30º,
以求得,yN=AN·sin30º=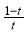 ,且xN=
,且xN=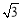 +AN·cos30º=
+AN·cos30º=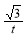 ,由此可得:
,由此可得: =(
=(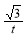 ,
,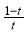 ),
),
又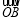 =(0, 1),⇒
=(0, 1),⇒ 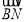 =
=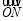 -
-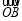 =(
=(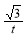 ,
,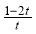 ).······ ⑶
).······ ⑶
由⑵,⑶两式得: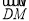 ·
·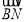 =2(
=2(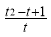 ),且|
),且|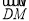 ||
||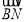 |=4(
|=4(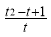 ).
).
故cos<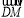 ,
,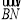 >=
>=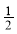 ,又<
,又<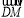 ,
,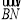 >∈[0,π] ⇒ <
>∈[0,π] ⇒ <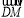 ,
,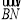 >=60º为所求.
>=60º为所求.
(2)由(1)知:f(t)=2(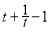 ),且由0<t<1知:f(t)>2⇒函数y=
),且由0<t<1知:f(t)>2⇒函数y=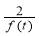 的值域为A=(0,1).
的值域为A=(0,1).
另由a>0知:函数y=g(t),t1∈(0,1)的值域为:B=(4-2a,4-a).
①若存在t1,t2∈(0,1),使得 =g(t2) 成立,则只要两函数的值域A=(0,1)与B=(4-2a,4-a)
=g(t2) 成立,则只要两函数的值域A=(0,1)与B=(4-2a,4-a)
存在公共元素即可.此时A与B间的关系有以下三种可能:
(1) A⊆B时,则必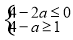 ⇒ 2≤a≤3;
⇒ 2≤a≤3;
(2) A∩B≠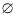 时,则0<4-2a<1,或0<4-a<1,⇒
时,则0<4-2a<1,或0<4-a<1,⇒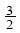 <a<2,或3<a<4;
<a<2,或3<a<4;
(iii) B⊆A时,则必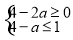 ⇒a无解. 综上,
⇒a无解. 综上,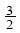 <a<4,为所求.
<a<4,为所求.
②对任意t1∈(0,1),恒存在t2∈(0,1),使得 =g(t2)成立,则t∈(0,1)时,函数y=g(t)必取遍函数y=
=g(t2)成立,则t∈(0,1)时,函数y=g(t)必取遍函数y=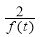 值域A=(0,1) 中的所有值,此即A⊆B,故由①知:2≤a≤3为所求.
值域A=(0,1) 中的所有值,此即A⊆B,故由①知:2≤a≤3为所求.

考点:函数的图象和性质,平面向量共线,夹角,数量积.


科目:高中数学 来源:2015届河北省石家庄市五校联合体高三上学期第一次月考理科数学试卷(解析版) 题型:选择题
若抛物线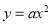 的准线的方程是
的准线的方程是 ,则实数a的值是( )
,则实数a的值是( )
A. B.
B. C.8 D.
C.8 D.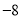
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三10月月考理科数学试卷(解析版) 题型:选择题
将函数y=sin x的图象上所有的点向右平移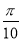 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是 ( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是 ( )
A.
B.
C.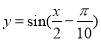
D.
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:解答题
(1)求 的值.
的值.
(2)已知6 sin2x+sinxcosx-2cos2x=0,π<x<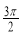 ,试求sin2x-cos2x+tan2x的值.
,试求sin2x-cos2x+tan2x的值.
查看答案和解析>>
科目:高中数学 来源:2015届江西省南昌市三校高三10月联考理科数学试卷(解析版) 题型:选择题
若函数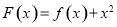 为奇函数,且g(x)= f(x)+2,若 f(1) =1,则g(-1)的值为:( )
为奇函数,且g(x)= f(x)+2,若 f(1) =1,则g(-1)的值为:( )
A.1 B.-1 C.2 D.-2
查看答案和解析>>
科目:高中数学 来源:2015届江苏省连云港高二下学期期末数学试卷(选修物理)(解析版) 题型:填空题
如果某年年份的各位数字之和为7,我们称该年为“七巧年”.例如,今年年份2014的各位数字之和为7,所以今年恰为“七巧年”.那么从2000年到2999年中“七巧年”共有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com