练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．设f（x）是R上的奇函数f（x+4）=f（x），当x∈[0，1]时，f（x）=3x，则f（11.5）=（　　）
    A．1.5B．0.5C．-1.5D．-0.5

    分析 先根据题意分析可得函数f（x）的周期为4，可得f（11.5）=f（-0.5+4×3）=f（-0.5），在结合函数的奇偶性可得f（-0.5）=-f（0.5），结合函数的解析式可得f（0.5）的值，综合可得答案．

    解答 解：根据题意，函数f（x）满足f（x+4）=f（x），即函数的周期为4，
    则有f（11.5）=f（-0.5+4×3）=f（-0.5），
    又由函数为奇函数，则f（-0.5）=-f（0.5），
    又由x∈[0，1]时，f（x）=3x，则f（0.5）=3×0.5=1.5；
    故f（11.5）=f（-0.5）=-f（-0.5）=-1.5；
    故选：C．

    点评 本题考查函数的奇偶性、周期性，关键是利用函数的周期性、奇偶性分析得到f（11.5）与f（0.5）的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    19．设0＜a＜1，若函数f（x）=ax+b的图象上每一点都不在第一象限，则实数b的最大值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知向量$\overrightarrow a=（{1-t，2t-1，3}）$，$\overrightarrow b=（{2，t，t}）$，则$|{\overrightarrow a-\overrightarrow b}|$的最小值为（　　）
    A．2B．$\sqrt{5}$C．$\sqrt{6}$D．$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知随机变量ξ服从正态分布N（0，σ2），若P（ξ＞3）=0.023，则P（-3≤ξ≤3）=（　　）
    A．0.954B．0.023C．0.977D．0.046

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．由经验得知，在某大商场付款处排队等候付款的人数及其概率如表：
    排队人数5人及以下678910人及以上
    概率0.10.160.30.30.10.04
    （1）不多于6个人排队的概率；
    （2）至少8个人排队的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若函数f（x）=ax2-（2a+1）x+a+1对于任意a∈[-1，1]，都有f（x）＜0，则实数x的取值范围是（1，2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

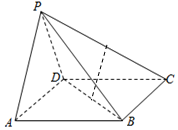    10．如图所示，在四棱锥P-ABCD中，四边形ABCD为矩形，△PAD为等腰三角形，∠APD=90°，平面PAD⊥平面ABCD，且AB=1，AD=2，E，F分别为PC，BD的中点．
    （1）证明：EF∥平面PAD；
    （2）证明：直线PA⊥平面PCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知正项等比数列{an}满足a7=a6+2a5，若存在两项am，an，使得$\sqrt{{a_m}{a_n}}=4{a_1}$，则$\frac{1}{m}+\frac{4}{n}$的最小值为（　　）
    A．$\frac{3}{2}$B．$\frac{4}{3}$C．$\frac{25}{6}$D．不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数f（x）=m（x+m+3）（x+m+2），g（x）=2x-2，若?x∈R，f（x）＜0或g（x）＜0恒成立，则实数m的取值范围为（　　）
    A．（-3，0）B．（-2，0）C．（-3，-2）D．（0，3）

    查看答案和解析>>

    同步练习册答案