
分析 (1)运用分段函数的各段的解析式,函数即可得到所求值;
(2)由等差数列的定义和通项公式,计算即可得到所求通项公式.
解答 解:(1)函数f(x)=$\left\{\begin{array}{l}{5,(0≤x≤1)}\\{f(x-1)+3,(x>1)}\end{array}\right.$,
可得f(2)=f(1)+3=5+3=8,
f(5)=f(4)+3=f(3)+6=f(2)+9=f(1)+12=5+12=17;
(2)当x>1,且x∈N*时,有f(x)-f(x-1)=3,
即有数列为5为首项,3为公差的等差数列,
可得通项公式为f(n)=f(1)+3(n-1)=5+3n-3=3n+2.
点评 本题考查分段函数的运用,注意运用分段函数的各段的解析式,同时考查等差数列的通项公式的运用,属于基础题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一个大风车的半径为8米,按逆时针方向12分钟旋转一周,它的最低点离地面高2米,如图所示,设风车翼片的一个端点P离地面的距离为h(m),P的初始位置在最低点.风车转动的时间为t(min),当t=8(min)时,h=14(m); h与t的函数关系为$h(t)=-8cos\frac{π}{6}t+10$.
一个大风车的半径为8米,按逆时针方向12分钟旋转一周,它的最低点离地面高2米,如图所示,设风车翼片的一个端点P离地面的距离为h(m),P的初始位置在最低点.风车转动的时间为t(min),当t=8(min)时,h=14(m); h与t的函数关系为$h(t)=-8cos\frac{π}{6}t+10$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
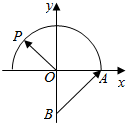 如图,已知点O(0,0),A(1,0),B(0,-1),P是曲线y=$\sqrt{1-{x}^{2}}$上一个动点,则$\overrightarrow{OP}$•$\overrightarrow{BA}$的取值范围是[-1,$\sqrt{2}$].
如图,已知点O(0,0),A(1,0),B(0,-1),P是曲线y=$\sqrt{1-{x}^{2}}$上一个动点,则$\overrightarrow{OP}$•$\overrightarrow{BA}$的取值范围是[-1,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com