
 将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法?
将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法? 分析 通过分种植的作物有“113型”和“122型”两种讨论,进而利用分步乘法计数原理计算即得结论.
解答 解:依题意,种植的作物有“113型”和“122型”两种情况:
①种植的作物为“113型”时:先挑出一种作物种植3块地,
然后利用插空法将剩下的两种作物分别中间,共有${C}_{3}^{1}$•${A}_{2}^{2}$=6种;
②种植的作物为“122型”时:先挑出只种植一块地的一种作物共${C}_{3}^{1}$种,
然后再挑出一种植物分别种在两端共${C}_{2}^{1}$种,最后再种植第三种作物共${C}_{4}^{2}$种,
于是,共有${C}_{3}^{1}$${C}_{2}^{1}$${C}_{4}^{2}$=36种;
由分类加法计数原理可知,共有6+36=42种种植方法.
点评 本题考查计数原理的应用,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{13π}{48},0)$ | B. | $(\frac{π}{8},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{7π}{12},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2544 | B. | 1332 | C. | 2532 | D. | 1320 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 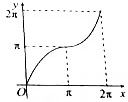 | C. | 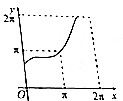 | D. | 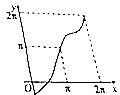 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com