
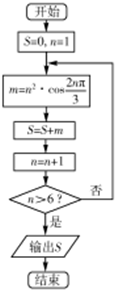
分析 模拟执行程序,依次写出每次循环得到的S,n的值,当n=7时满足条件,退出循环,输出S的值为22.
解答 解:模拟运行程序,可得初始值S=0,n=1,
第1次进入循环体,m=-$\frac{1}{2}$×12,S=-$\frac{1}{2}$×12,n=2,判定为否;
第2次进入循环体,m=-$\frac{1}{2}$×22,S=-$\frac{1}{2}$×12-$\frac{1}{2}×{2}^{2}$,n=3,判定为否;
第3次进入循环体,m=1×32,S=-$\frac{1}{2}$×12-$\frac{1}{2}×{2}^{2}$+1×32,n=4,判定为否;
…
第6次进入循环体,m=1×62,S=-$\frac{1}{2}$×12-$\frac{1}{2}×{2}^{2}$+1×32$-\frac{1}{2}×{4}^{2}-\frac{1}{2}×{5}^{2}+1×{6}^{2}$,n=7,判定为是;
退出循环,输出S=-$\frac{1}{2}×({1}^{2}+{2}^{2}+{4}^{2}+{5}^{2})+{3}^{2}+{6}^{2}$=22.
故答案为:22.
点评 本题主要考查了循环结构的程序框图,意在考查学生分析问题和解决问题的能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{9}{20}$ | D. | $\frac{5}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=4 | B. | x=-2 | C. | x=-4 | D. | x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若ac=bc(c≠0),则a=b”类比推出“若$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$($\overrightarrow{c}$≠$\overrightarrow{0}$),则$\overrightarrow{a}$=$\overrightarrow{b}$” | |
| B. | “在实数中有(a+b)c=ac+bc”类比推出“在向量中($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$” | |
| C. | “在实数中有(ab)c=a(bc)”类比推出“在向量中($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)” | |
| D. | “若ab=0,则a=0或b=0”类比推出“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
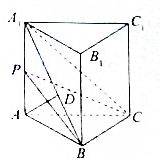 如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=2$\sqrt{3}$,CB⊥AB,D为线段A1B上一点,且A1D=3,P为AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=2,AA1=2$\sqrt{3}$,CB⊥AB,D为线段A1B上一点,且A1D=3,P为AA1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com