

| A. | $28+4\sqrt{3}+12\sqrt{2}$ | B. | $36+4\sqrt{3}+12\sqrt{2}$ | C. | $36+4\sqrt{2}+12\sqrt{3}$ | D. | $44+12\sqrt{2}$ |
分析 由三视图还原原几何体如图,该几何体下底面是等腰直角三角形,直角边为4,上底面是等腰直角三角形,直角边为2$\sqrt{2}$.CG⊥底面ABC,CG⊥底面EFG.然后结合三角形、正方形及梯形面积求解.
解答 解:由三视图还原原几何体如图: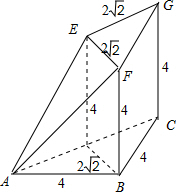
下底面是等腰直角三角形,直角边为4,上底面是等腰直角三角形,直角边为2$\sqrt{2}$.
CG⊥底面ABC,CG⊥底面EFG.
可求得AE=AF=4$\sqrt{2}$.
∴等腰三角形AEF底边上的高为$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}=2\sqrt{6}$.
∴该几何体的表面积为S=$\frac{1}{2}×4×4+\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$$+\frac{1}{2}×4×4+4×4+\frac{1}{2}×2\sqrt{2}×2\sqrt{6}$$+\frac{1}{2}(2\sqrt{2}+4\sqrt{2})×4$=$36+4\sqrt{3}+12\sqrt{2}$.
故选:B.
点评 本题考查几何体的三视图,关键是由三视图还原原几何体,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{36}-\frac{y^2}{16}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}-\frac{y^2}{36}=1$ |
查看答案和解析>>
科目:高中数学 来源:2017届湖北省协作校高三联考一数学(理)试卷(解析版) 题型:选择题
已知命题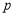 :对任意
:对任意 ,
,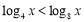 ,命题
,命题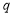 :存在
:存在 ,使得
,使得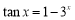 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A.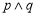 B.
B.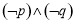
C.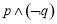 D.
D.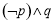
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com