考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(空间向量)依条件可知AB,AC,AA
1两两垂直.以点A为原点,建立空间直角坐标系A-xyz.求出相关点的坐标,
(Ⅰ)利用
•=0,得到
⊥.通过
是平面ACC
1A
1的一个法向量,推出MN∥平面ACC
1A
1.
(Ⅱ)求出平面ABC的法向量是
=(x,y,z),利用法向量与向量
=(-,0,-2)的夹角,求解所求线面所成角的余弦值.
(逻辑推理)(Ⅰ)作出AC的中点D,连结DN,A
1D.通过证明四边形A
1DNM是平行四边形,得到MN∥A
1D,利用直线与平面平行的判定定理证明MN∥平面ACC
1A
1.
(Ⅱ)作出AB的中点F说明∠MNF就是所求的线面所成角,解三角形即可.
解答:
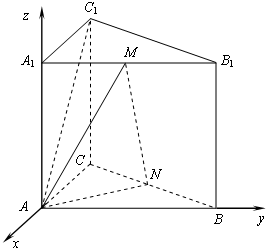
解:(空间向量)依条件可知AB,AC,AA
1两两垂直.如图,
以点A为原点,建立空间直角坐标系A-xyz.
依条件可知AB,AC,AA
1两两垂直.
如图,以点A为原点,建立空间直角坐标系A-xyz.
根据条件容易求出如下各点坐标:A(0,0,0),B(0,2,0),C(-1,0,0),A
1(0,0,2),B
1(0,2,2),C
1(-1,0,2),M(0,1,2),
N(-,1,0).
(Ⅰ)因为
=(0,2,0),
=(-1,0,2),
因为
=(-,0,-2),
=(0,2,0),所以
•=
-×0+0×2-2×0=0,
从而
⊥.
又因为
=(0,2,0)是平面ACC
1A
1的一个法向量,且MN?平面ACC
1A
1,
所以MN∥平面ACC
1A
1.
(Ⅱ)
=(-1,-2,0),
=(0,2,0)设平面ABC的法向量是
=(x,y,z)由
•=0,
•=0,知法向量可以是
=(0,0,1),它与向量
=(-,0,-2)的夹角满足:
cosθ==-,
所以所求线面所成角的余弦值是
.
(逻辑推理)(Ⅰ)如图
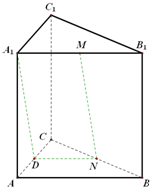
作出AC的中点D,连结DN,A
1D.
∵D,N分别是AC,BC的中点
∴DN∥AB且DN=
AB,
∵ABC-A
1B
1C
1是三棱柱,
∴AB∥A
1B
1且AB=A1BA
又∵M是A
1B
1的中点,
∴A1M=
A1B1=
AB=DN,
∵DN∥AB,AB∥A
1B
1∴DN∥A
1M∴四边形A
1DNM是平行四边形
∴MN∥A
1D
∵MN?平面ACC1,A
1A
1D?平面ACC
1A
1∴MN∥平面ACC
1A
1.
(Ⅱ)如图

作出AB的中点F∵N,F分别是BC,AB的中点∴NF∥AC,NF=
AC=
又∵M是A
1B
1的中点,
∴MF∥AA
1,MF=AA
1=2
∵三棱柱ABC-A
1B
1C
1的侧棱垂直于底面,
∴MF⊥面ABC,MF⊥NF
∴∠MNF就是所求的线面所成角.
∴
cosMEN===
点评:本题用两种方法证明直线与平面平行,直线与平面所成角的求法,考查空间想象能力以及计算能力,转化思想的应用.

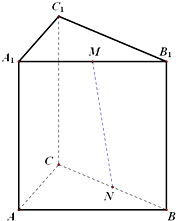 已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.
已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点. 解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,
解:(空间向量)依条件可知AB,AC,AA1两两垂直.如图,



 如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2
如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2