
 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
分析 (1)由频率分布直方图各小长方形面积总和为1,建立方程,即可求得结论;
(2)利用组中值,求出对应销售收益的平均值;
(3)利用公式求出b,a,即可计算y关于x的回归方程.
解答 解:(1)设各小长方形的宽度为m,由频率分布直方图中各小长方形的面积总和为1,可知(0.08+0.1+0.14+0.12+0.04+0.02)•m=0.5m=1,故m=2,即图中各小长方形的宽度为2.…(3分)
(2)由(1)知各小组依次是[0,2),[2,4),[4,6),[6,8),[8,10),[10,12],
其中点分别为1,3,5,7,9,11,
对应的频率分别为0.16,0.20,0.28,0.24,0.08,0.04,
故可估计平均值为1×0.16+3×0.2+5×0.28+7×0.24+9×0.08+11×0.04=5.…(7分)
(3)由(2)可知空白栏中填5.
由题意可知,$\overline{x}=\frac{1+2+3+4+5}{5}=3,\overline{y}=\frac{2+3+2+5+7}{5}=3.8$,$\sum_{i=1}^5{x_i}{y_i}=1×2+2×3+3×2+4×5+5×7=69$,$\sum_{i=1}^5x_i^2={1^2}+{2^2}+{3^2}+{4^2}+{5^2}=55$,
根据公式,可求得$\hat b=\frac{69-5×3×3.8}{{55-5×{3^2}}}=\frac{12}{10}=1.2$,…(10分)$\hat a=3.8-1.2×3=0.2$,…(11分)
所以所求的回归直线方程为y=1.2x+0.2.…(12分)
点评 本题考查频率分布直方图,考查线性回归方程的求法和应用,本题解题的关键是看出这组变量是线性相关的,进而正确运算求出线性回归方程的系数,本题是一个中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
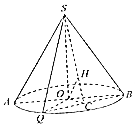 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com