练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．某公司未来对一种新产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
    单价x（元）456789
    销量y（件）908483807568
    由表中数据，求得线性回归方程为$\hat y=-4x+\hat a$，当产品销量为76件时，产品定价大致为7.5元．

    分析 计算样本中心，代入回归方程解出a，得到回归方程，y=76代入，可得结论．

    解答 解：$\overline{x}$=6.5，$\overline{y}$=80，
    ∴$\stackrel{∧}{a}$=80-（-4）×6.5a=106，
    ∴回归方程为$\stackrel{∧}{y}$=-4x+106．
    y=76时，76=-4x+106，∴x=7.5，
    故答案为7.5．

    点评 本题考查了线性回归方程的性质，利用线性回归方程进行预测，古典概型的概率计算，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=$\frac{2}{x}$-2+2alnx．
    （1）讨论函数f（x）的单调性；
    （2）若f（x）在区间[$\frac{1}{2}$，2]上的最小值为0，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某公司为了解广告投入对销售收益的影响，在若干地区各投入4万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）．由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的．[附：回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
    （1）根据频率分布直方图计算图中各小长方形的宽度；
    （2）试估计该公司投入4万元广告费用之后，对应销售收益的平均值（以各组的区间中点值代表该组的取值）；
    （3）该公司按照类似的研究方法，测得另外一些数据，并整理得到下表：
    广告投入x（单位：万元）12345
    销售收益y（单位：万元）2327
    由表中的数据显示，x与y之间存在着线性相关关系，请将（2）的结果填入空白栏，并求出y关于x的回归直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知等差数列{an}为各项均为正数，其前n项和为Sn，若a1=1，$\sqrt{{S}_{3}}$=a2，则a8=（　　）
    A．12B．13C．14D．15

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=sinωx+$\sqrt{3}$cosωx（ω＞0）在（$\frac{π}{6}$，$\frac{π}{2}$）上单调，且满足f（$\frac{π}{6}$）+f（$\frac{π}{2}$）=0，则ω=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．数列{an}的前项和记为Sn，a1=t，点（an+1，Sn）在直线$y=\frac{1}{2}x-1$上n∈N+．
    （1）当实数t为何值时，数列{an}是等比数列？并求数列{an}的通项公式；
    （2）若f（x）=[x]（[x]表示不超过x的最大整数），在（1）的结论下，令${b_n}=f（{log_3}{a_n}）+1，{c_n}={a_n}+\frac{1}{{{b_n}{b_{n+2}}}}$，求{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知点F（3，0）是双曲线3x2-my2=3m（m＞0）的一个焦点，则此双曲线的离心率为$\frac{\sqrt{6}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

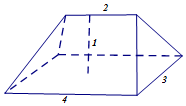    5．《九章算术》卷第五《商功》中，有问题“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈．问积几何？”，意思是：“今有底面为矩形的屋脊状的楔体，下底面宽3丈，长4丈；上棱长2丈，无宽，高1丈（如图）．
    问它的体积是多少？”这个问题的答案是（　　）
    A．5立方丈B．6立方丈C．7立方丈D．9立方丈

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）离心率为$\sqrt{3}$，左右焦点分别为F1，F2，P为双曲线右支上一点，∠F1PF2的平分线为l，点F1关于l的对称点为Q，|F2Q|=2，则双曲线方程为（　　）
    A．$\frac{{x}^{2}}{2}$-y2=1B．x2-$\frac{{y}^{2}}{2}$=1C．x2-$\frac{{y}^{2}}{3}$=1D．$\frac{{x}^{2}}{3}$-y2=1

    查看答案和解析>>

    同步练习册答案