
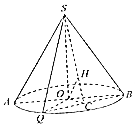
 如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.
如图,圆锥的横截面为等边三角形SAB,O为底面圆圆心,Q为底面圆周上一点.分析 (Ⅰ)连接OC,AQ,由已知可得OC∥AQ,再由AB为圆的直径,可得OC⊥BQ,由SO⊥平面ABQ,得SO⊥BQ,由线面垂直的判定可得BQ⊥平面SOC,进一步得到平面SBQ⊥平面SOC,由面面垂直的性质可OH⊥平面SBQ;
(Ⅱ)由已知求解三角形可得OQ=OA=2,SA=4,则SO=$\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$.由已知体积公式求得圆锥的体积.
解答 (Ⅰ)证明:连接OC,AQ,
∵O为AB的中点,且BQ的中点为C,
∴OC∥AQ,
∵AB为圆的直径,∠AQB=90°,∴OC⊥BQ,
∵SO⊥平面ABQ,∴SO⊥BQ,
又SO∩OC=O,∴BQ⊥平面SOC,
则平面SBQ⊥平面SOC,
又平面SBQ∩平面SOC=SC,OH⊥SC,
∴OH⊥平面SBQ;
(Ⅱ)解:∵∠AOQ=60°,QB=2$\sqrt{3}$,∴OC=1,OQ=OA=2,SA=4,
则SO=$\sqrt{{4}^{2}-{2}^{2}}=2\sqrt{3}$.
∴圆锥的体积V=$\frac{1}{3}π{r}^{2}•h=\frac{1}{3}π×{2}^{2}×2\sqrt{3}=\frac{8\sqrt{3}}{3}π$.
点评 本题考查直线与平面垂直的判定,考查空间想象能力和思维能力,训练了圆锥体积的求法,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
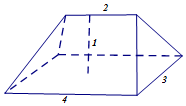 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).| A. | 5立方丈 | B. | 6立方丈 | C. | 7立方丈 | D. | 9立方丈 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | [1,2] | C. | {0,1,2,4} | D. | [0,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{3})$ | B. | $(-\frac{1}{3},+∞)$ | C. | (3,+∞) | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{2}$-y2=1 | B. | x2-$\frac{{y}^{2}}{2}$=1 | C. | x2-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$-y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com