
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
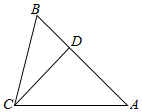 △ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.
△ABC中,B=$\frac{π}{3}$,点D在边AB上,BD=1,且DA=DC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1-2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$-1) | C. | (2$\sqrt{2}$-1,+∞) | D. | (1-2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某新建公司规定,招聘的职工须参加不小于80小时的某种技能培训才能上班.公司人事部门在招聘的职工中随机抽取200名参加这种技能培训的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com