
分析 利用向量加法和向量减法的平行四边形法则,及数乘向量的几何意义,可得相应的向量.
解答 解:(1)$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$+$\overrightarrow{OB}$)如下图所示:
(2)$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OA}$-$\overrightarrow{OB}$)如下图所示:
(3)$\overrightarrow{OG}$=3$\overrightarrow{OA}$+2$\overrightarrow{OB}$如下图所示:
点评 本题考查的知识点是向量加减运算及数乘运算的几何意义,向量加法和向量减法的平行四边形法则,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<2} | B. | {-1,0,1} | C. | {0,1,2} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
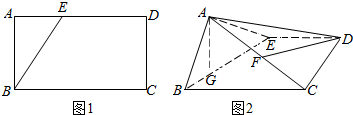
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
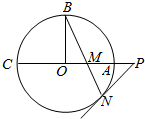 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图所示,在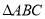 中,
中,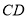 是
是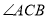 的角平分线,
的角平分线,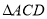 的外接圆交
的外接圆交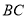 于
于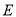 点.
点.
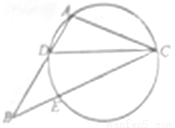
(1)证明: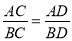 ;
;
(2)若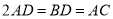 ,求
,求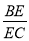 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com