
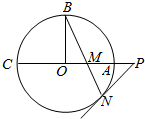
 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P分析 (1)连接ON,则ON⊥PN,由半径相等可得OB=ON,可得∠OBM=∠ONB,利用切线的性质和已知可得∠BOM=∠ONP=90°,进而可得∠PMN=∠PNM,再利用切割线定理即可证明;
(2)由相交弦定理得⊙O的半径,再求劣弧$\widehat{BN}$的长.
解答 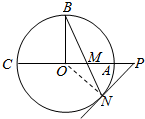 (1)证明:连结ON,则ON⊥PN,且△OBN为等腰三角形,则∠OBN=∠ONB,
(1)证明:连结ON,则ON⊥PN,且△OBN为等腰三角形,则∠OBN=∠ONB,
∵∠PMN=∠OMB=90°-∠OBN,
∠PNM=90°-∠ONB,
∴∠PMN=∠PNM,∴PM=PN.
根据切割线定理,有PN2=PA•PC,
∴PM2=PA•PC.…(5分)
(2)解:设$OM=x∴OA=\sqrt{3}x$,则在直角△OBM中,BM=2x
又$MA=\sqrt{3}x-x,CM=\sqrt{3}x+x$,由相交弦定理得$2x×2=(\sqrt{3}x+x)•(\sqrt{3}x-x)∴x=2$
故⊙O的半径$r=2\sqrt{3}$,
∴BN弧长$l=2\sqrt{3}•\frac{2π}{3}=\frac{{4\sqrt{3}π}}{3}$…(10分)
点评 本题综合考查了圆的切线的性质、切割线定理、相交弦定理等基础知识,考查了分析问题和解决问题的能力、推理能力和计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,\frac{1}{2})$ | B. | [$\frac{1}{2}$,$\frac{5}{2}$] | C. | $[{\frac{1}{2},2})$ | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com