
科目:高中数学 来源: 题型:解答题
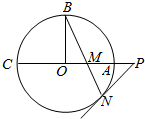 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图所示,在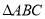 中,
中,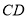 是
是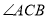 的角平分线,
的角平分线,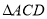 的外接圆交
的外接圆交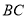 于
于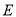 点.
点.
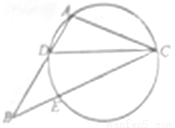
(1)证明: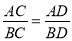 ;
;
(2)若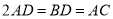 ,求
,求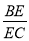 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
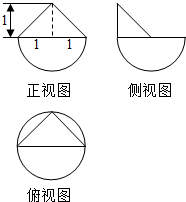 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+2$\sqrt{2}$-1 | B. | 3π+2$\sqrt{2}$ | C. | 2π+2$\sqrt{2}$-1 | D. | 2π+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com