
分析 根据题意,画出图形,结合图形建立空间直角坐标系,以棱长1为一个长度单位,表示出点的坐标,求出向量$\overrightarrow{AB}$、$\overrightarrow{GC}$、$\overrightarrow{GD}$和$\overrightarrow{AE}$的坐标表示,设$\overrightarrow{AE}$=x$\overrightarrow{AB}$+y$\overrightarrow{GC}$+z$\overrightarrow{GD}$,求出对应的x、y、z的值,再化为$\overrightarrow{AB}$、$\overrightarrow{GC}$和$\overrightarrow{GD}$方向上的单位向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{{e}_{3}}$即可得出向量$\overrightarrow{AE}$的坐标.
解答 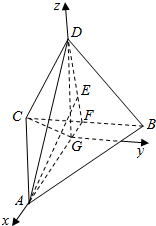 解:根据题意,画出图形,如图所示;
解:根据题意,画出图形,如图所示;
正四面体ABCD的顶点D在底面ABC你的射影是底面△ABC的中心G,以点G为坐标原点,以GA为x轴,GD为z轴,以过点G且平行于CB的限直线为y轴,建立空间直角坐标系,且AB=1,
F是BC的中点,
∴AF=$\frac{\sqrt{3}}{2}$,∴GA=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,∴GF=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{6}$;
∴GC=GA=$\frac{\sqrt{3}}{3}$,GD=$\sqrt{{1}^{2}{-(\frac{\sqrt{3}}{3})}^{2}}$=$\frac{\sqrt{6}}{3}$;
∴G(0,0,0),A($\frac{\sqrt{3}}{3}$,0,0),B(-$\frac{\sqrt{3}}{6}$,$\frac{1}{2}$,0),C(-$\frac{\sqrt{3}}{6}$,-$\frac{1}{2}$,0),
D(0,0,$\frac{\sqrt{6}}{3}$),E(-$\frac{\sqrt{3}}{9}$,0,$\frac{\sqrt{6}}{9}$),F(-$\frac{\sqrt{3}}{6}$,0,0);
∴$\overrightarrow{AB}$=(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),$\overrightarrow{GC}$=(-$\frac{\sqrt{3}}{6}$,-$\frac{1}{2}$,0),
$\overrightarrow{GD}$=(0,0,$\frac{\sqrt{6}}{3}$),$\overrightarrow{AE}$=(-$\frac{4\sqrt{3}}{9}$,0,$\frac{\sqrt{6}}{9}$);
设$\overrightarrow{AE}$=x$\overrightarrow{AB}$+y$\overrightarrow{GC}$+z$\overrightarrow{GD}$,x、y、z∈R;
则(-$\frac{4\sqrt{3}}{9}$,0,$\frac{\sqrt{6}}{9}$)=(-$\frac{\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{6}$y,$\frac{1}{2}$x-$\frac{1}{2}$y,$\frac{\sqrt{6}}{3}$z),
即$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{2}x-\frac{\sqrt{3}}{6}y=-\frac{4\sqrt{3}}{9}}\\{\frac{1}{2}x-\frac{1}{2}y=0}\\{\frac{\sqrt{6}}{3}z=\frac{\sqrt{6}}{9}}\end{array}\right.$,
解得x=y=$\frac{2}{3}$,z=$\frac{1}{3}$;
∴$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{GC}$+$\frac{1}{3}$$\overrightarrow{GD}$;
又$\overrightarrow{AE}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{GC}$=$\frac{\sqrt{3}}{3}$$\overrightarrow{{e}_{2}}$,$\overrightarrow{GD}$=$\frac{\sqrt{6}}{3}$$\overrightarrow{{e}_{3}}$,
∴$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{{e}_{1}}$+$\frac{2}{3}$×$\frac{\sqrt{3}}{3}$$\overrightarrow{{e}_{2}}$+$\frac{1}{3}$×$\frac{\sqrt{6}}{3}$$\overrightarrow{{e}_{3}}$=$\frac{2}{3}$$\overrightarrow{{e}_{1}}$+$\frac{2\sqrt{3}}{9}$$\overrightarrow{{e}_{2}}$+$\frac{\sqrt{6}}{9}$$\overrightarrow{{e}_{3}}$;
∴向量$\overrightarrow{AE}$的坐标是($\frac{2}{3}$,$\frac{2\sqrt{3}}{9}$,$\frac{\sqrt{6}}{9}$).
故答案为:($\frac{2}{3}$,$\frac{2\sqrt{3}}{9}$,$\frac{\sqrt{6}}{9}$).
点评 本题考查了空间向量的应用问题,也考查了向量的坐标表示与解方程组的应用问题,考查了数形结合的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
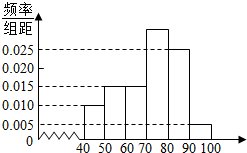 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com