
分析 (1)将f(f(x))进行化简,看结果是否含有θ;
(2)利用第一问结论脱函数符号进行计算.
解答 解:(1)f(f(x))=x-2(x•$\overrightarrow{a}$)$\overrightarrow{a}$-2[(x-2(x•$\overrightarrow{a}$)$\overrightarrow{a}$)$•\overrightarrow{a}$]$\overrightarrow{a}$=x-2(x•$\overrightarrow{a}$)$\overrightarrow{a}$-2[x$•\overrightarrow{a}$-2(x$•\overrightarrow{a}$)]$\overrightarrow{a}$=x-2(x•$\overrightarrow{a}$)$\overrightarrow{a}$+2(x$•\overrightarrow{a}$)$\overrightarrow{a}$=x,
∴当θ的取值范围变化时,f(f(x))不发生变化.
(2)∵f[f($\overrightarrow{m}$+2$\overrightarrow{n}$)]=$\overrightarrow{m}+2\overrightarrow{n}$,f(f(2$\overrightarrow{m}$-$\overrightarrow{n}$)]=2$\overrightarrow{m}-\overrightarrow{n}$,∴$\overrightarrow{m}+2\overrightarrow{n}$⊥2$\overrightarrow{m}-\overrightarrow{n}$,
即($\overrightarrow{m}+2\overrightarrow{n}$)•(2$\overrightarrow{m}-\overrightarrow{n}$)=0,∴2$\overrightarrow{m}$2-3$\overrightarrow{m}•\overrightarrow{n}$-2$\overrightarrow{n}$2=0,解得$\overrightarrow{m}•\overrightarrow{n}$=$\frac{5}{2}$,
设$\overrightarrow{m},\overrightarrow{n}$夹角为θ,则cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=1.∴$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{2}$.
点评 本题考查了平面向量的运算化简及数量积运算,注意|$\overrightarrow{a}$|=1是关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x0∈z,1<4x0<3 | B. | ?x0∈z,4x0+1=0 | C. | ?x∈R,x2-1=0 | D. | ?x∈R,x2-2x+2≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
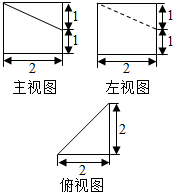
| A. | $\frac{23}{3}$ | B. | 4$\sqrt{2}$+$\sqrt{6}$+6 | C. | 6$\sqrt{2}$+6 | D. | 4$\sqrt{2}$+$\sqrt{6}$+8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com