
分析 先分析出该极限是一个“$\frac{0}{0}$”型极限,从而确定a的值,再对分子因式分解,化简后再求其极限.
解答 解:当x→-1时,分母x+1→0,
且原式极限存在,所以该极限是“$\frac{0}{0}$”型极限,
因此,当x=-1时,分子等于零,
即-1-a+1+4=0,解得a=4,所以,
原式=$\underset{lim}{x→-1}$$\frac{x^3-4x^2-x+4}{x+1}$
=$\underset{lim}{x→-1}$$\frac{(x+1)(x-1)(x-4)}{x+1}$
=$\underset{lim}{x→-1}$(x-1)(x-4)
=(-2)×(-5)=10,
所以,a=4,A=10.
点评 本题主要考查了极限及其运算,尤其是要分析出该极限是“$\frac{0}{0}$”型极限,考查了多项式的因式分解,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,2] | C. | {0,1,2} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.
已知扇形AOB的圆心角∠AOB=$\frac{π}{6}$,半径OA=1,在$\widehat{AB}$上有一个动点M,过M作矩形MNPQ,如图,设∠AOM=θ,记矩形MNPQ的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
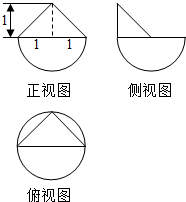 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 3π+2$\sqrt{2}$-1 | B. | 3π+2$\sqrt{2}$ | C. | 2π+2$\sqrt{2}$-1 | D. | 2π+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com