
(本小题满分10分)已知直线的参数方程为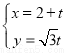 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为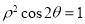 .
.
(1)求曲线C的直角坐标方程;
(2)直线l被曲线C截得的弦长.
(1)x2-y2=1;(2)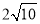 .
.
【解析】
试题分析:(1)应用余弦的二倍角公式将曲线C的极坐标方程化为含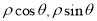 的式子,然后应用公式
的式子,然后应用公式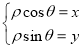 即可求出曲线C的普通方程;(2)将直线的参数方程化为普通方程,联立曲线C的普通方程,消元得到一个一元二次方程,再用韦达定理及弦长公式就可就出所求的弦长.
即可求出曲线C的普通方程;(2)将直线的参数方程化为普通方程,联立曲线C的普通方程,消元得到一个一元二次方程,再用韦达定理及弦长公式就可就出所求的弦长.
试题解析:(1)由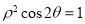 得
得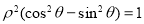 ,
, 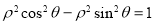 ,
,
∵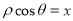 ,
,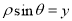 ,∴x2-y2=1.
,∴x2-y2=1.
(2)消去参数t可得,直线l的方程为y=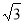 (x-2)
(x-2)
将y=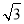 (x-2)代入x2-y2=1得
(x-2)代入x2-y2=1得
2x2-12x+13=0
解得x1=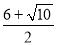 ,x2=
,x2=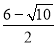
∴弦长为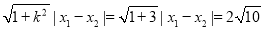 .
.
考点:参数方程,极坐标方程与直线与圆的位置关系.
考点分析: 考点1:参数方程 试题属性

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查文科数学试卷(解析版) 题型:解答题
已知椭圆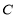 :
: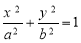 (
(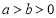 )过点(2,0),且椭圆C的离心率为
)过点(2,0),且椭圆C的离心率为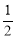 .
.
(Ⅰ)求椭圆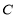 的方程;
的方程;
(Ⅱ)若动点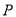 在直线
在直线 上,过
上,过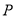 作直线交椭圆
作直线交椭圆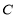 于
于 两点,且
两点,且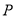 为线段
为线段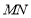 中点,再过
中点,再过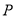 作直线
作直线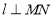 .求直线
.求直线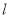 是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省福州市高三毕业班第六次质量检查理科数学试卷(解析版) 题型:选择题
对于函数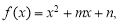 若
若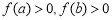 ,则函数
,则函数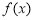 在区间
在区间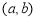 内
内
A.一定有零点 B.一定没有零点
C.可能有两个零点 D.至多有一个零点
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期期末考试数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为 ( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)设椭圆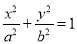 (a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2,
(a>b>0)的左右焦点分别为F1、F2,点D在椭圆上,DF1⊥F1F2,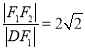 ,△DF1F2的面积为
,△DF1F2的面积为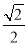 .
.
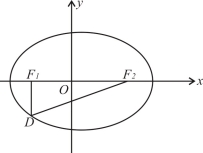
(1)求该椭圆的标准方程;
(2)若圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点,求出这个圆的方程.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省高二上学期期末考试文科数学试卷(解析版) 题型:选择题
若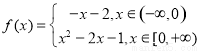 ,x1<x2<x3,且f (x1)=f (x2)=f (x3),则x1+x2+x3的值的范围是( )
,x1<x2<x3,且f (x1)=f (x2)=f (x3),则x1+x2+x3的值的范围是( )
A.[1, 2) B.(1, 2] C.(0, 1] D.[2, 3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省高二上学期期末考试文科数学试卷(解析版) 题型:选择题
曲线f(x)=x3-2x+1在点(1, 0)处的切线方程为( )
A.y=-x+1 B.y=x-1 C.y=2x-2 D.y=-2x+2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知双曲线C: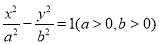 ,F是双曲线C的右焦点,点A是渐近线上第一象限内的一点,O为坐标原点,且|OA|=
,F是双曲线C的右焦点,点A是渐近线上第一象限内的一点,O为坐标原点,且|OA|=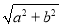 ,若
,若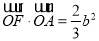 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.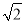 B.
B.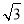 C.2 D.
C.2 D.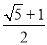
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com