练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若求O的半径为4，且球心O到平面α的距离为$\sqrt{3}$，则平面α截球O所得截面圆的面积为（　　）
    A．πB．10πC．13πD．52π

    分析 根据球的半径R、球心距，求出截面圆半径，可得截面面积．

    解答 解：作出对应的截面图∵球的半径R=4，由球心距d=$\sqrt{3}$
    故截面圆半径r=$\sqrt{{4}^{2}-3}=\sqrt{13}$=1
    故截面圆面积S=πr2=13π
    故选：C．

    点评 本题考查球性质，点到平面的距离，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．教材曾有介绍：圆x2+y2=r2上的点（x0，y0）处的切线方程为x0x+y0y=r2．我们将其结论推广：椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上的点（x0，y0）处的切线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1，在解本题时可以直接应用．已知，直线x-y+$\sqrt{3}$=0与椭圆C1：$\frac{x^2}{a^2}+{y^2}$=1（a＞1）有且只有一个公共点．
    （1）求椭圆C1的方程；
    （2）设O为坐标原点，过椭圆C1上的两点A、B分别作该椭圆的两条切线l1、l2，且l1与l2交于点M（2，m）．当m变化时，求△OAB面积的最大值；
    （3）若P1，P2是椭圆C2：$\frac{x^2}{{2{a^2}}}+{y^2}$=1上不同的两点，P1P2⊥x轴，圆E过P1，P2，且椭圆C2上任意一点都不在圆E内，则称圆E为该椭圆的一个内切圆．试问：椭圆C2是否存在过左焦点F1的内切圆？若存在，求出圆心E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知集合A={（x，y）|3x+y=0}，B={（x，y）|2x-y=3}，则A∩B=（$\frac{3}{5}$，-$\frac{9}{5}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．为了了解高血压是否与常喝酒有关，现对30名成年人进行了问卷调查得到如下列联表：
    常喝不常喝合计
    正常血压4812
    高血压16218
    合计201030
    已知在全部30人中随机抽取1人，抽到正常血压成年人的概率为$\frac{2}{5}$．
    （1）请将上面的列联表补充完整；
    （2）是否有99%的把握认为高血压与常喝酒有关？说明理由；
    （3）4名调查人员随机分成两组，每组2人，一组负责问卷调查，另一组负责数据处理，求工作人员甲分到负责收集数据组，工作人员乙分到负责数据处理组的概率．
    参考数据：
    P（K2≥k）0.150.100.050.0250.0100.0050.001
    k2.0722.7063.8415.0246.6357.87910.828
    （参考公式：K2=$\frac{{n（ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．函数$y=sin\frac{1}{2}x$（　　）
    A．在[-π，π]上是增函数B．在[0，π]上是减函数
    C．在$[{-\frac{π}{2}，\frac{π}{2}}]$上是减函数D．在[-π，0]上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知P（x，y）满足$\left\{\begin{array}{l}{x≤2}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$，则z=x-y最小值是-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

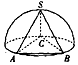    14．如图，已知底面为正三角形，侧棱长都相等的三棱锥S-ABC各顶点都在半球面上，其中A、B、C三顶点在底面圆周上，若三棱锥S-ABC的体积为2$\sqrt{3}$，则该半球的体积为$\frac{16π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设等差数列{an}的前n项和为Sn，若a1+a13=4，则S1326．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某学校为了制定治理学校门口上学，放学期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查，得到了如下的列联表（单位：人）
    同一限定区域停车不同一限定区域停车合计
    男5
    女10
    合计50
    已知在抽取的50分调查问卷中速记抽取一份，抽到不同意限定区域停车问卷的概率为$\frac{2}{5}$．
    （1）请将上面的列联表补充完整；
    （2）是否有99.5%的把握恩威是否同意限定区域停车与家长的性别有关？请说明理由．
    附临界表及参考公式：
    P（K2≥k0）0.150.100.050.0250.0100.0050.001
    k02.0722.7063.8415.0246.6357.87910.828
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．

    查看答案和解析>>

    同步练习册答案