
分析 化简函数的解析式,根据函数的解析式可得它的图象的对称性.
解答 解:函数f(x)=$\frac{x}{x+1}$+$\frac{x+1}{x+2}$+$\frac{x+2}{x+3}$=1-$\frac{1}{x+1}$+1-$\frac{1}{x+2}$+1-$\frac{1}{x+3}$=3-($\frac{1}{x+1}$+$\frac{1}{x+2}$+$\frac{1}{x+3}$),
它的定义域为{x|x≠-1,x≠-2,x≠-3},$\frac{-1+(-3)}{2}$=-2.
又 f(-4-x)=3+($\frac{1}{x+1}$+$\frac{1}{x+2}$+$\frac{1}{x+3}$),∴f(x)+f(-4-x)=6,
故f(x)的图象的对称中心为(-2,3),
故答案为:(-2,3).
点评 本题主要考查函数的图象的对称性,考查转化思想以及计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{13}}{2}$] | B. | ($\frac{\sqrt{13}}{2}$,$\sqrt{17}$) | C. | (0,$\sqrt{17}$) | D. | (0,$\frac{5\sqrt{2}}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
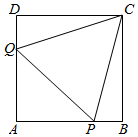 某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.
某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y-1=0 | B. | x+2y+2=0 | C. | x+2y+1=0 | D. | x+2y+3=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com