Question

10．在平行四边形中，AC与BD交于点O，$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{DO}$，CE的延长线与AD交于点F，若$\overrightarrow{CF}$=$λ\overrightarrow{AC}$+$μ\overrightarrow{BD}$（λ，μ∈R），则λ+μ=-$\frac{1}{3}$．

Answer 1

分析 利用三角形的相似关系，求得$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{BD}$，再根据向量的加法的三角形法则，求得λ和μ的值．

解答 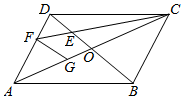解：∵△FED∽△CEB，
DF：CD=DE：EA=1：3，
过点F作FG∥BD交AC于G，
FG：DO=2：3，
AG：AO=2：3，
∴$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{BD}$，
∵$\overrightarrow{CG}$=$\overrightarrow{CO}$+$\overrightarrow{OG}$=$\frac{2}{3}\overrightarrow{CA}$，
∴$\overrightarrow{CF}=\overrightarrow{AG}+\overrightarrow{GF}$=$\frac{2}{3}\overrightarrow{CA}$+$\frac{1}{3}$$\overrightarrow{BD}$，
$\overrightarrow{CF}$=$-\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}$，
λ+μ=-$\frac{1}{3}$．
故答案为：-$\frac{1}{3}$．

点评 本题考查根据三角形的相似关系，求得三角各边的比值，再根据向量加法的三角形法则，求得其和向量，属于中档题．