
| A. | (-20,0] | B. | [-20,0] | C. | [-20,0) | D. | (-20,0) |
分析 由切线的对称性和圆的知识将问题转化为C(2,1)到直线3x+4y+a=0的距离小于或等于2,再由点到直线的距离公式得到关于a的不等式求解.
解答 解:圆(x-2)2+(y-1)2=2的圆心为:C(2,1),半径为$\sqrt{2}$,
∵直线3x+4y+a=0上存在点M使得过P的圆C的两条切线互相垂直,
∴在直线上存在一点M,使得P到C(0,0)的距离等于2,
∴只需C(2,1)到直线3x+4y+a=0的距离小于或等于2,
故$\frac{|10+a|}{5}$≤2,解得-20≤a≤0,
故选:B.
点评 本题考查直线和圆的位置关系,由题意得到C(2,1)到直线3x+4y+a=0的距离小于或等于2是解决问题的关键,属中档题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{2x}({x>0})$的图象上.若点Bn的坐标为(n,0)(n∈N*),记矩形AnBnCnDn的周长为an,则a1+a2+…+a10( )| A. | 208 | B. | 212 | C. | 216 | D. | 220 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | $({\frac{3}{4},2}]$ | C. | $[{\frac{3}{4},2})$ | D. | $({\frac{1}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
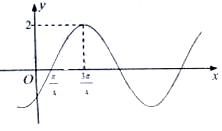
| A. | $φ=-\frac{π}{4}$ | |
| B. | 函数f(x)在$[{-\frac{π}{4},\frac{3π}{4}}]$上单调递增 | |
| C. | 函数f(x)的一条对称轴是$x=\frac{3π}{4}$ | |
| D. | 为了得到函数f(x)的图象,只需将函数y=2cosx的图象向右平移$\frac{π}{4}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com