
分析 (Ⅰ)若f1(1)=3,则a+a-1=3,结合a+a-1=(${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$)2-2可得答案;
(Ⅱ)若fk(x)为定义在R上的奇函数,且a>1,则k=-1,fk(x)=ax-a-x在R上为增函数,故问题可转化为:λ<$\frac{5-cos2x}{2sinx}$=$\frac{2{sin}^{2}x+4}{2sinx}$=sinx+$\frac{2}{sinx}$对任意x∈[0,$\frac{2π}{3}$]恒成立,结合对勾函数的图象和性质,可得答案.
解答 解:(Ⅰ)若f1(1)=3,
则a+a-1=(${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$)2-2=3,
∴(${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$)2=5,
∴${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$=$\sqrt{5}$,或${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$=-$\sqrt{5}$(舍去),
则f1($\frac{1}{2}$)=${a}^{\frac{1}{2}}+{a}^{-\frac{1}{2}}$=$\sqrt{5}$,
(Ⅱ)若fk(x)为定义在R上的奇函数,
则fk(0)=a+ka=0,
解得:k=-1,
∵a>1,
∴fk(x)=ax-a-x在R上为增函数,
则fk(cos2x)+fk(2λsinx-5)<0可化为:fk(cos2x)<-fk(2λsinx-5)=fk(5-2λsinx),
即cos2x<5-2λsinx对任意x∈[0,$\frac{2π}{3}$]恒成立,
即λ<$\frac{5-cos2x}{2sinx}$=$\frac{2{sin}^{2}x+4}{2sinx}$=sinx+$\frac{2}{sinx}$对任意x∈[0,$\frac{2π}{3}$]恒成立,
令t=sinx,(t∈[0,1]),
则y=t+$\frac{2}{t}$为减函数,当t=1时,y取最小值3,
故λ<3.
点评 本题考查的知识点是函数恒成立问题,函数的最值,对勾函数的图象和性质,函数求值,难度中档.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-20,0] | B. | [-20,0] | C. | [-20,0) | D. | (-20,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
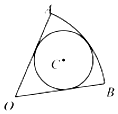 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若在扇形AOB内任取一点,则该点在圆C内的概率为$\frac{2}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com