
分析 2α=8⇒α=3,则f(x)=x3.若P真:f(2-a)>f(a-1),利用函数f(x)的单调性可得a范围;若Q真:2a-1>1,利用指数函数的单调性可得a-1>0,解得a范围.由P∧Q为真,求其交集即可.
解答 解:∵2α=8⇒α=3,则f(x)=x3,
若P真:f(2-a)>f(a-1),$⇒2-a>a-1⇒a<\frac{3}{2}$;
若Q真:2a-1>1,∴a-1>0,解得a>1.
∵P∧Q为真,
∴$\left\{{\begin{array}{l}{a<\frac{3}{2}}\\{a>1}\end{array}}\right.⇒1<a<\frac{3}{2}$.
∴实数a的取值范围是$(1,\frac{3}{2})$.
点评 本题考查了复合命题真假的判定、函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
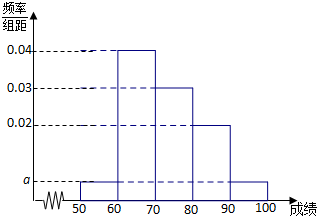 某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校1000名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 4:5 | 3:2 | 2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com