Question

10．若函数f（x）=sin（x-$\frac{π}{6}$）的图象如图所示，则图中的阴影部分的面积为$\frac{2-\sqrt{3}}{2}$．

Answer 1

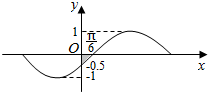
分析 根据积分的应用，进行求解面积即可．

解答 解：由积分的几何意义得${∫}_{0}^{\frac{π}{6}}$[0-sin（x-$\frac{π}{6}$）]dx=${∫}_{0}^{\frac{π}{6}}$（$\frac{1}{2}$cosx-$\frac{\sqrt{3}}{2}$sinx）dx
=（$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx）|${\;}_{0}^{\frac{π}{6}}$=$\frac{1}{2}sin$$\frac{π}{6}$+$\frac{\sqrt{3}}{2}×$cos$\frac{π}{6}$-$\frac{\sqrt{3}}{2}$cos0
=$\frac{1}{2}×\frac{1}{2}+\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}$=1-$\frac{\sqrt{3}}{2}$=$\frac{2-\sqrt{3}}{2}$，
故答案为：$\frac{2-\sqrt{3}}{2}$

点评 本题主要考查导数的应用，利用积分求面积是解决本题的关键．