
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时直线
取得最大值时直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
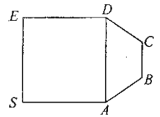
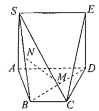
【题目】某产品的包装纸可类比如图所示的平面图形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包装的过程中,沿着
,在包装的过程中,沿着![]() 将正方形
将正方形![]() 折起,直至
折起,直至![]() ,得到多面体
,得到多面体![]() ,
,![]() 分别为
分别为![]() 中点.
中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新冠疫情,某企业组织员工进行用款捐物的爱心活动.原则上每人以自愿为基础,捐款不超过400元.现项目负责人统计全体员工数据后,下表为随机抽取的10名员工.的捐款数额.
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
捐款数额 | 124 | 86 | 215 | 53 | 132 | 195 | 400 | 90 | 300 | 225 |
(1)若从这10名员工中任意选取3人,记选到的3人中捐款数额大于200元的人数为X,求X的分布列和数学期望:
(2)以表中选取的10人作为样本.估计该企业全体员工的捐款情况,现从企业员工中依次抽取8人,若抽到k人的捐款数额小于200元的可能性最大,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
区间 |
|
|
|
|
|
人数 | 50 | 50 | a | 150 | b |

(1)上表是年龄的频数分布表,求正整数![]() 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com