
【题目】为抗击新冠疫情,某企业组织员工进行用款捐物的爱心活动.原则上每人以自愿为基础,捐款不超过400元.现项目负责人统计全体员工数据后,下表为随机抽取的10名员工.的捐款数额.
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
捐款数额 | 124 | 86 | 215 | 53 | 132 | 195 | 400 | 90 | 300 | 225 |
(1)若从这10名员工中任意选取3人,记选到的3人中捐款数额大于200元的人数为X,求X的分布列和数学期望:
(2)以表中选取的10人作为样本.估计该企业全体员工的捐款情况,现从企业员工中依次抽取8人,若抽到k人的捐款数额小于200元的可能性最大,求k的值.
【答案】(1)分布列见详解,![]() ;(2)5
;(2)5
【解析】
(1)由题中的随机分布表可知,10名员工中,捐款数额大于200元的有4人,![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,![]() 服从超几何分布,由此能求出
服从超几何分布,由此能求出![]() 的概率分布列及数学期望;
的概率分布列及数学期望;
(2)从8人中抽取的捐款数额小于200元的人数为随机变量![]() ,则
,则![]() ,假设
,假设![]() 最大,可列出不等式组,求出
最大,可列出不等式组,求出![]() 的值.
的值.
解:(1)由题知,10名员工中,捐款数额大于200元的有4人,
则随机变量![]() 服从超几何分布,
服从超几何分布,![]() 的所有可能取值为0,1,2,3
的所有可能取值为0,1,2,3
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
则![]() 的分布列为
的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() ;
;
(2)以样本估计总体的捐款金额小于200的概率![]() ,
,
设![]() 为从8人中抽取的捐款数额小于200元的人数,
为从8人中抽取的捐款数额小于200元的人数,![]() ,
,
![]() ,
,
要使其取得最大值,则需:
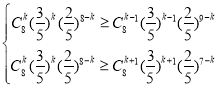 ,
,
解得![]() ,
,
又![]() ,故
,故![]() ,
,
即依次抽取8人,若抽到5人的捐款数额小于200元的可能性最大.


科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送每张面额为
向用户随机派送每张面额为![]() 元,
元,元,
![]() 元的 三种骑行券.用户每次使用
元的 三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得
扫码用车后,都可获得一张骑行券.用户骑行一次获得![]() 元券,获得
元券,获得![]() 元券的概率分别是
元券的概率分别是![]() ,
,![]() ,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时直线
取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆节期间,滕州市实验小学举行了一次科普知识竞赛活动,设置了一等奖、二等奖、三等奖、四等奖及纪念奖,获奖人数的分配情况如图所示,各个奖品的单价分别为:一等奖50元、二等奖20元、三等奖10元,四等奖5元,纪念奖2元,则以下说法中不正确的是( )
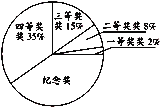
A.获纪念奖的人数最多B.各个奖项中二等奖的总费用最高
C.购买奖品的费用平均数为6.65元D.购买奖品的费用中位数为5元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,椭圆
,椭圆![]() 的上、下顶点分别为
的上、下顶点分别为![]() ,
,![]() ,左、右顶点分别为
,左、右顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() .原点到直线
.原点到直线![]() 的距离为
的距离为![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆上异于
是椭圆上异于![]() ,
,![]() 的任一点,直线
的任一点,直线![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() ,
,![]() ,若直线
,若直线![]() 与过点
与过点![]() ,
,![]() 的圆
的圆![]() 相切,切点为
相切,切点为![]() ,证明:线段
,证明:线段![]() 的长为定值,并求出该定值.
的长为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过抛物线y2=2px(p>0)上一点P(1,2),作两条直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时:
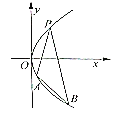
(1)求y1+y2的值;
(2)若直线AB在y轴上的截距b∈[﹣1,3]时,求△ABP面积S△ABP的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com