
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】毕达哥拉斯树是由毕达哥拉斯根据“勾股定理”所画出来的一个可以无限重复的图形,也叫“勾股树”,其是由一个等腰直角三角形分别以它的每一条边向外作正方形而得到.图1所示是第1代“勾股树”,重复图1的作法,得到第2代“勾股树”(如图2),如此继续.若“勾股树”上共得到8191个正方形,设初始正方形的边长为1,则最小正方形的边长为( )
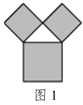
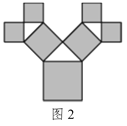
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富学生课外生活,某市组织了高中生钢笔书法比赛,比赛分两个阶段进行:第一阶段由评委给出所有参赛作品评分,并确定优胜者;第二阶段为附加赛,参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析,这些分数![]() 都在
都在![]() 内,在以组距为5画分数的频率分布直方图(设“
内,在以组距为5画分数的频率分布直方图(设“![]() ”)时,发现
”)时,发现![]() 满足
满足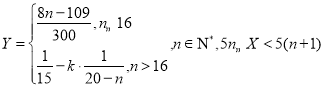 .
.
(1)试确定![]() 的所有取值,并求
的所有取值,并求![]() ;
;
(2)组委会确定:在第一阶段比赛中低于85分的参赛者无缘获奖也不能参加附加赛;分数在![]() 的参赛者评为一等奖;分数在
的参赛者评为一等奖;分数在![]() 的同学评为二等奖,但通过附加赛有
的同学评为二等奖,但通过附加赛有![]() 的概率提升为一等奖;分数在
的概率提升为一等奖;分数在![]() 的同学评为三等奖,但通过附加赛有
的同学评为三等奖,但通过附加赛有![]() 的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生
的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生![]() 和
和![]() 均参加了本次比赛,且学生
均参加了本次比赛,且学生![]() 在第一阶段评为二等奖.
在第一阶段评为二等奖.
(![]() )求学生
)求学生![]() 最终获奖等级不低于学生
最终获奖等级不低于学生![]() 的最终获奖等级的概率;
的最终获奖等级的概率;
(![]() )已知学生
)已知学生![]() 和
和![]() 都获奖,记
都获奖,记![]() 两位同学最终获得一等奖的人数为
两位同学最终获得一等奖的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为2019年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊5个民生项目,得到如下信息:
①若该地区引进甲项目,就必须引进与之配套的乙项目;
②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;
③乙、丙两个项目之间有冲突,两个项目只能引进一个;
④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;
⑤若引进项目戊,甲、丁两个项目也必须引进.
则该地区应引进的项目为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送每张面额为
向用户随机派送每张面额为![]() 元,
元,元,
![]() 元的 三种骑行券.用户每次使用
元的 三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得
扫码用车后,都可获得一张骑行券.用户骑行一次获得![]() 元券,获得
元券,获得![]() 元券的概率分别是
元券的概率分别是![]() ,
,![]() ,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是菱形,AC=BC=2,∠CBB1=![]() ,点A在平面BCC1B1上的投影为棱BB1的中点E.
,点A在平面BCC1B1上的投影为棱BB1的中点E.
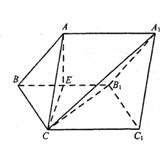
(1)求证:四边形ACC1A1为矩形;
(2)求二面角E-B1C-A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某传染病疫情爆发期间,当地政府积极整合医疗资源,建立“舱医院”对所有密切接触者进行14天的隔离观察治疗.治疗期满后若检测指标仍未达到合格标准,则转入指定专科医院做进一步的治疗.“舱医院”对所有人员在“入口”及“出口”时都进行了医学指标检测,若“入口”检测指标在35以下者则不需进入“舱医院”而是直接进入指定专科医院进行治疗.以下是20名进入“舱医院”的密切接触者的“入口”及“出口”医学检测指标:
入口 | 50 | 35 | 35 | 40 | 55 | 90 | 80 | 60 | 60 | 60 | 65 | 35 | 60 | 90 | 35 | 40 | 55 | 50 | 65 | 50 |
出口 | 70 | 50 | 60 | 50 | 75 | 70 | 85 | 70 | 80 | 70 | 55 | 50 | 75 | 90 | 60 | 60 | 65 | 70 | 75 | 70 |
(Ⅰ)建立![]() 关于
关于![]() 的回归方程;(回归方程的系数精确到0.1)
的回归方程;(回归方程的系数精确到0.1)
(Ⅱ)如果60是“舱医院”的“出口”最低合格指标,那么,“入口”指标低于多少时,将来这些密切接触者将不能进入“舱医院”而是直接进入指定专科医院接受治疗.(检测指标为整数)
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: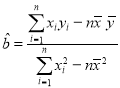 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时直线
取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com