
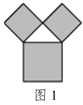
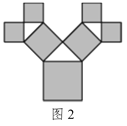
【题目】毕达哥拉斯树是由毕达哥拉斯根据“勾股定理”所画出来的一个可以无限重复的图形,也叫“勾股树”,其是由一个等腰直角三角形分别以它的每一条边向外作正方形而得到.图1所示是第1代“勾股树”,重复图1的作法,得到第2代“勾股树”(如图2),如此继续.若“勾股树”上共得到8191个正方形,设初始正方形的边长为1,则最小正方形的边长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 且
且![]() ,圆
,圆![]() ,点
,点![]() ,
,![]() 是圆
是圆![]() 上的动点,线段
上的动点,线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)讨论曲线![]() 的形状,并求其方程;
的形状,并求其方程;
(2)若![]() ,且
,且![]() 面积的最大值为
面积的最大值为![]() ,直线
,直线![]() 过点
过点![]() 且不垂直于坐标轴,
且不垂直于坐标轴,![]() 与曲线
与曲线![]() 交于
交于![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() (任意项都不为零)的前
(任意项都不为零)的前![]() 项和为
项和为![]() ,首项为
,首项为![]() ,对于任意
,对于任意![]() ,满足
,满足![]() .
.
(1)数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() 使得
使得![]() 成等比数列,且
成等比数列,且![]() 成等差数列?若存在,试求
成等差数列?若存在,试求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设数列![]() ,
, ,若由
,若由![]() 的前
的前![]() 项依次构成的数列是单调递增数列,求正整数
项依次构成的数列是单调递增数列,求正整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作斜率为
作斜率为![]() 的直线恰好与椭圆
的直线恰好与椭圆![]() 有且仅有一个公共点.
有且仅有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆
为椭圆![]() 的长轴上的一个动点,过点
的长轴上的一个动点,过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于不同的两点
于不同的两点![]() ,
,![]() ,是否存在常数
,是否存在常数![]() ,使
,使![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是1990年-2017年我国劳动年龄(15-64岁)人口数量及其占总人口比重情况:
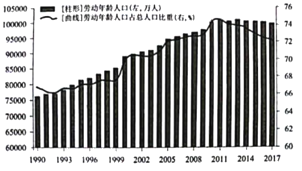
根据图表信息,下列统计结论不正确的是( )
A. 2000年我国劳动年龄人口数量及其占总人口比重的年增幅均为最大
B. 2010年后我国人口数量开始呈现负增长态势
C. 2013年我国劳动年龄人口数量达到峰值
D. 我国劳动年龄人口占总人口比重极差超过![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,
,
且![]() ,
,![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)设数列![]() 满足
满足![]() ,
,![]()
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com