
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,若对
,若对![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为2019年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊5个民生项目,得到如下信息:
①若该地区引进甲项目,就必须引进与之配套的乙项目;
②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;
③乙、丙两个项目之间有冲突,两个项目只能引进一个;
④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;
⑤若引进项目戊,甲、丁两个项目也必须引进.
则该地区应引进的项目为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春季气温逐渐攀升,病菌滋生传播快,为了确保安全开学,学校按30名学生一批,组织学生进行某种传染病毒的筛查,学生先到医务室进行血检,检呈阳性者需到防疫部门]做进一步检测.学校综合考虑了组织管理、医学检验能力等多万面的因素,根据经验,采用分组检测法可有效减少工作量,具体操作如下:将待检学生随机等分成若干组,先将每组的血样混在一起化验,若结果呈阴性,则可断定本组血样合格,不必再做进一步的检测;若结果呈阳性,则本组中的每名学生再逐个进行检测.现有两个分组方案:方案一:将30人分成5组,每组6人;方案二:将30人分成6组,每组5人.已知随机抽一人血检呈阳性的概率为0.5%,且每个人血检是否呈阳性相互独立.
(Ⅰ)请帮学校计算一下哪一个分组方案的工作量较少?
(Ⅱ)已知该传染疾病的患病率为0.45%,且患该传染疾病者血检呈阳性的概率为99.9%,若检测中有一人血检呈阳性,求其确实患该传染疾病的概率.(参考数据:(![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: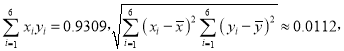
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为
的横坐标为![]() ,
,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最大值,并求
的最大值,并求![]() 取得最大值时直线
取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的准线上一点,F为抛物线的焦点,P为抛物线上的点,且
的准线上一点,F为抛物线的焦点,P为抛物线上的点,且![]() ,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
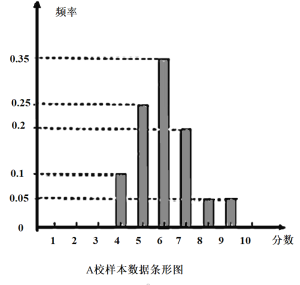
B校样本数据统计表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,F是E的右焦点,过点F的直线交E于点
,F是E的右焦点,过点F的直线交E于点![]() 和点
和点![]() (
(![]() ).当直线
).当直线![]() 与x轴垂直时,
与x轴垂直时,![]() .
.
(1)求椭圆E的方程;
(2)设直线l:![]() 交x轴于点G,过点B作x轴的平行线交直线l于点C.求证:直线
交x轴于点G,过点B作x轴的平行线交直线l于点C.求证:直线![]() 过线段
过线段![]() 的中点.
的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com