
分析 得出f(0)=0,f(1)=2,当0<x<1时,f(x)=2+$\frac{2}{x-1+\frac{2}{x-1}+2}$x∈(0,1),运用对钩函数的单调性求解得出0<2+$\frac{2}{x-1+\frac{2}{x-1}+2}$<2,即可求解值域.
解答  解:∵函数f(x)=$\frac{2{x}^{2}+2x}{{x}^{2}+1}$,
解:∵函数f(x)=$\frac{2{x}^{2}+2x}{{x}^{2}+1}$,
x=0时,f(0)=0,x=1时,f(1)=2,
当0<x<1时,f(x)=2+$\frac{2}{x-1+\frac{2}{x-1}+2}$,
∵x-1+$\frac{2}{x-1}$<-3,
∴x-1$+\frac{2}{x-1}$+2<-1,
∴-1<$\frac{2}{x-1+\frac{2}{x-1}+2}$<0,
即0<2+$\frac{2}{x-1+\frac{2}{x-1}+2}$<2,
综上f(x)在[0,1]上的值域[0,2]
点评 本题考查了分式函数的值域的求解,关键是恒等变形得出不等式条件,运用对钩函数的性质求解,考查了学生的恒等变形能力.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
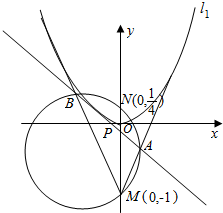 如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.
如图,已知抛物线C:y=ax2(a>0)与射线l1:y=2x-1(x≥0)、l2:y=-2x-1(x≤0)均只有一个公共点,过定点M(0,-1)和N(0,$\frac{1}{4}$)的动圆分别与l1、l2交于点A、B,直线AB与x轴交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{4}$ | C. | $\frac{11}{4}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在(-∞,+∞)上是增函数 | |
| B. | 在(-∞,+∞)上是减函数 | |
| C. | 在(-∞,0]上是增函数,在[0,+∞)上是减函数 | |
| D. | 在(-∞,0]上是减函数,在[0,+∞)上是增函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com