
分析 分类常数化简可得y=$\frac{1}{2}$(1+$\frac{{a}^{2}-1}{2acosx+{a}^{2}+1}$),易得a2-1<0,由函数的单调性可得.
解答 解:化简可得y=$\frac{a(cosx+a)}{2acosx+{a}^{2}+1}$
=$\frac{acosx+{a}^{2}}{2acosx+{a}^{2}+1}$=$\frac{1}{2}$•$\frac{2acosx+{a}^{2}+1+{a}^{2}-1}{2acosx+{a}^{2}+1}$
=$\frac{1}{2}$(1+$\frac{{a}^{2}-1}{2acosx+{a}^{2}+1}$),
∵a∈(0,1),∴a2-1<0,
当cosx=-1时,函数取最大值$\frac{a}{a-1}$;
当cosx=1时,函数取最小值$\frac{a}{a+1}$.
点评 本题考查三角函数的最值,整体分类常数是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
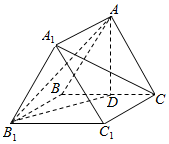 如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.
如图,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,$SA=AB=BC=2,tan∠SDA=\frac{2}{3}$.
如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,$SA=AB=BC=2,tan∠SDA=\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
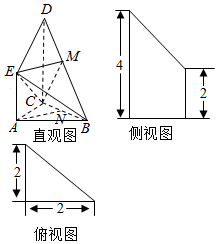 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,3) | B. | (-5.25,-5) | C. | [-5,5) | D. | 前三个都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com