
| A. | 若f(x0)是f(x)的极值,则f(x)在x0处可导且f′(x0)=0 | |
| B. | 若曲线y=f(x)在x0附近的左侧切线斜率为正,右侧切线斜率为负,则f(x0)是f(x)的极大值 | |
| C. | 若曲线y=f(x)在x0附近的左侧切线斜率为负,右侧切线斜率为正,则f(x0)是f(x)的极大值 | |
| D. | 若f′(x0)=0,则f(x0)必是f(x)的极值 |
分析 根据函数的性质分别对各个选项进行判断即可.
解答 解:若函数y=f(x)在点x=x0处有极值,则f(x)在x0处可导且f′(x0)=0,故A正确;
若曲线y=f(x)在x0附近的左侧切线斜率为正,右侧切线斜率为负,
则f(x0)不一定是f(x)的极大值,如y=$\frac{1}{x}$,故B错误;
若曲线y=f(x)在x0附近的左侧切线斜率为负,右侧切线斜率为正,
则f(x0)不一定是f(x)的极大值,如y=-$\frac{1}{x}$,故C错误;
若f′(x0)=0,则f(x0)不一定是f(x)的极值,如y=x3,故D错误;
故选:A.
点评 本题考查了函数的连续性、函数的极值问题,是一道基础题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
 某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.
某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (0,2) | C. | (-2,1) | D. | (-2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
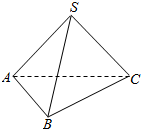 如图,在棱长都相等的四面体SABC中,给出如下三个命题:
如图,在棱长都相等的四面体SABC中,给出如下三个命题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$.
已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com