
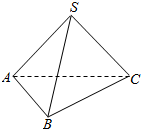
 如图,在棱长都相等的四面体SABC中,给出如下三个命题:
如图,在棱长都相等的四面体SABC中,给出如下三个命题:分析 ①根据线面垂直性质可判断;
②根据公式cosθ=cosθ1cosθ2求解即可;
③找出二面角的平面角,利用余弦定理求解.
解答 解:①取AB中点M,
易证AB垂直平面SMC,可得AB垂直SC,故错误;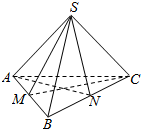
②易知BC在平面上的射影为∠ABC的角平分线,
∴cos60°=cosθcos30°,
∴cosθ=$\frac{\sqrt{3}}{3}$,故正确;
③取BC中点N,
∴二面角为∠ANC,不妨设棱长为1,
∴cos∠ANC=$\frac{\frac{3}{4}+\frac{3}{4}-1}{2×\frac{3}{4}}$=$\frac{1}{3}$,故正确,
故答案为:②③.
点评 考查了线面垂直,线面角,二面角的求法.属于基础题型.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | [-$\frac{1}{4}$,+∞) | D. | ($\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x0)是f(x)的极值,则f(x)在x0处可导且f′(x0)=0 | |
| B. | 若曲线y=f(x)在x0附近的左侧切线斜率为正,右侧切线斜率为负,则f(x0)是f(x)的极大值 | |
| C. | 若曲线y=f(x)在x0附近的左侧切线斜率为负,右侧切线斜率为正,则f(x0)是f(x)的极大值 | |
| D. | 若f′(x0)=0,则f(x0)必是f(x)的极值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
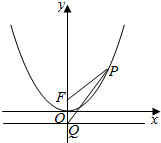 如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.
如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com