
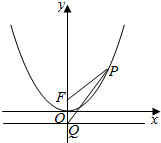
 如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2.
如图,设抛物线x2=4y的焦点为F,其准线与y轴相交于点Q,设P为抛物线上的一点,若$|{PQ}|=\sqrt{2}|{PF}|$,则△PQF的面积为2. 分析 求出抛物线的焦点和准线方程,求得Q(0,-1),设P(m,$\frac{1}{4}$m2),运用两点的距离公式,解方程可得m=2,运用三角形的面积公式,计算即可得到所求值.
解答 解:抛物线x2=4y的焦点为F(0,1),准线y=-1,
由题意可得Q(0,-1),
设P(m,$\frac{1}{4}$m2),由|PQ|=$\sqrt{2}$|PF|,
可得$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}+1)^{2}}$=$\sqrt{2}$•$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$,
解得m=2,
则△PQF的面积为$\frac{1}{2}$|FQ|•|xP|=$\frac{1}{2}$×2×2=2.
故答案为:2.
点评 本题考查抛物线的方程和性质,考查两点的距离公式的运用,考查运算能力,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
 如图,在棱长都相等的四面体SABC中,给出如下三个命题:
如图,在棱长都相等的四面体SABC中,给出如下三个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=cos(2x+\frac{π}{3})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com