
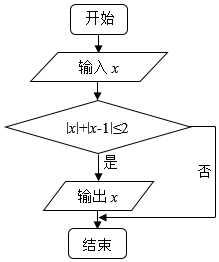
 如图所示的程序框图中,x∈[-2,2],则能输出x的概率为$\frac{1}{2}$.
如图所示的程序框图中,x∈[-2,2],则能输出x的概率为$\frac{1}{2}$. 分析 由|x|+|x-1|≤2α,可解得:x∈[-$\frac{1}{2}$,$\frac{3}{2}$],即当x∈[-$\frac{1}{2}$,$\frac{3}{2}$]时满足框图的条件,能输出x的值,结合x∈[-2,2],利用几何概型即可计算得解.
解答 解:∵|x|+|x-1|≤2α,
∴$\left\{\begin{array}{l}{x<0}\\{-x+(1-x)≤2}\end{array}\right.$,或$\left\{\begin{array}{l}{0≤x<1}\\{x+1-x≤2}\end{array}\right.$,或$\left\{\begin{array}{l}{x≥1}\\{x+x-1≤2}\end{array}\right.$,
∴解得:-$\frac{1}{2}$≤x<0,或0≤x<1,或1≤x≤$\frac{3}{2}$,即x∈[-$\frac{1}{2}$,$\frac{3}{2}$]时满足框图的条件,能输出x的值.
∵x∈[-2,2],
∴能输出x的概率为:$\frac{\frac{3}{2}-(-\frac{1}{2})}{2-(-2)}$=$\frac{1}{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查了几何概型,程序框图的综合应用,考查了分类讨论思想和计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1002×2015)2 | B. | (1008×2015)2 | C. | (2014×2015)2 | D. | (2016×2015)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
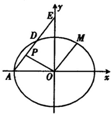 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,且点(1,$\frac{2\sqrt{2}}{3}$)在椭圆上,经过椭圆的左顶点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,且点(1,$\frac{2\sqrt{2}}{3}$)在椭圆上,经过椭圆的左顶点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com