
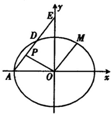
 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{2\sqrt{2}}{3}$���ҵ㣨1��$\frac{2\sqrt{2}}{3}$������Բ�ϣ�������Բ����A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E��
��ͼ����ƽ��ֱ������ϵxOy�У���֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{2\sqrt{2}}{3}$���ҵ㣨1��$\frac{2\sqrt{2}}{3}$������Բ�ϣ�������Բ����A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E������ ��1������Բ�������ʺ͵㣨1��$\frac{2\sqrt{2}}{3}$������Բ�ϣ��������������ʽ���a��b��ֵ������ԲC�ı����̿���
��2����i��ֱ��l�ķ���Ϊy=k��x+3��������Բ�������ã�1+9k2��x2+54k2x+81k2-9=0���ɴ�����Τ�ﶨ����ֱ�ߴ�ֱ�������������������
��ii��OM�ķ��̿���Ϊy=kx������Բ������M��ĺ�����Ϊx=��$\frac{3}{\sqrt{1+9{k}^{2}}}$����OM��l����$\frac{|AD|+|AE|}{|OM|}$ת��Ϊ��ĺ�����Ĺ�ϵ��ô𰸣�
��� �⣺��1���������֪��$\left\{\begin{array}{l}{\frac{c}{a}=\frac{2\sqrt{2}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{\frac{1}{{a}^{2}}+\frac{8}{9{b}^{2}}=1}\end{array}\right.$����ã�a2=9��b2=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{9}+{y}^{2}=1$��
��2����i��ֱ��l�ķ���Ϊy=k��x+3����
��$\left\{\begin{array}{l}{y=k��x+3��}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$���ã�1+9k2��x2+54k2x+81k2-9=0��
��x1=-3��${x}_{2}=\frac{3-27{k}^{2}}{1+9{k}^{2}}$��
��x=$\frac{3-27{k}^{2}}{1+9{k}^{2}}$ʱ��y=k��$\frac{3-27{k}^{2}}{1+9{k}^{2}}$+3��=$\frac{6k}{1+9{k}^{2}}$��
��D��$\frac{3-27{k}^{2}}{1+9{k}^{2}}$��$\frac{6k}{1+9{k}^{2}}$����
�ߵ�PΪAD���е㣬��P������Ϊ��$\frac{-27{k}^{2}}{1+9{k}^{2}}��\frac{3k}{1+9{k}^{2}}$����
��${k}_{OP}=-\frac{1}{9k}$��k��0����
ֱ��l�ķ���Ϊy=k��x+3������x=0����E������Ϊ��0��3k����
������ڶ���Q��m��n����m��0����ʹ��OP��EQ��
��kOPkEQ=-1����-$\frac{1}{9k}$•$\frac{n-3k}{m}$=-1�������
�ࣨ9m+3��k-n=0�������
��$\left\{\begin{array}{l}{9m+3=0}\\{-n=0}\end{array}\right.$����$\left\{\begin{array}{l}{m=-\frac{1}{3}}\\{n=0}\end{array}\right.$��
�ඨ��Q������Ϊ��-$\frac{1}{3}$��0����
��ii����OM��l����OM�ķ��̿���Ϊy=kx��
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{9}+{y}^{2}=1}\\{y=kx}\end{array}\right.$����M��ĺ�����Ϊx=��$\frac{3}{\sqrt{1+9{k}^{2}}}$��
��OM��l����$\frac{|AD|+|AE|}{|OM|}$=$\frac{|{x}_{D}-{x}_{A}|+|{x}_{E}-{x}_{A}|}{|{x}_{M}|}$
=$\frac{{x}_{D}-2{x}_{A}}{|{x}_{M}|}$=$\frac{\frac{3-27{k}^{2}}{1+9{k}^{2}}+6}{\frac{3}{\sqrt{1+9{k}^{2}}}}$=$\frac{3+9{k}^{2}}{\sqrt{1+9{k}^{2}}}$=$\sqrt{1+9{k}^{2}}+\frac{2}{\sqrt{1+9{k}^{2}}}$$��2\sqrt{2}$��
���ҽ���$\sqrt{1+9{k}^{2}}=\frac{2}{\sqrt{1+9{k}^{2}}}$����k=��$\frac{1}{3}$ʱȡ�Ⱥţ�
k=-$\frac{1}{3}$����ȥ����
�൱k=$\frac{1}{3}$ʱ��$\frac{|AD|+|AE|}{|OM|}$����СֵΪ$2\sqrt{2}$��
���� ���⿼����Բ���̵����������������Ķ����Ƿ���ڵ��ж������������ʽ����Сֵ����ע��Τ�ﶨ����ֱ�ߴ�ֱ����Բ���ʵĺ������ã����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x����x��x1 | B�� | x��x1��f��x�� | C�� | x��f��x����x1 | D�� | x��x2��f��x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
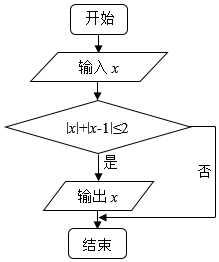 ��ͼ��ʾ�ij����ͼ�У�x��[-2��2]���������x�ĸ���Ϊ$\frac{1}{2}$��
��ͼ��ʾ�ij����ͼ�У�x��[-2��2]���������x�ĸ���Ϊ$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 15 | C�� | 20 | D�� | 28 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
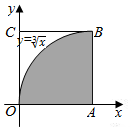
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��4] | B�� | ��$\frac{1}{2}$��1] | C�� | ��0��$\frac{1}{2}$] | D�� | ��-�ޣ�$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com