
【题目】设Sn是数列{an}的前n项和,且a1=1,an+1=﹣SnSn+1 , 则使 ![]() 取得最大值时n的值为明 .
取得最大值时n的值为明 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】锐角△ABC中,其内角A,B满足:2cosA=sinB﹣ ![]() cosB.
cosB.
(1)求角C的大小;
(2)D为AB的中点,CD=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
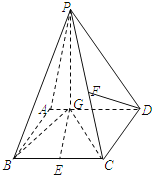
【题目】如图四棱锥![]() 中,底面ABCD是平行四边形,
中,底面ABCD是平行四边形,![]() 平面ABCD,垂足为G,G在AD上,且
平面ABCD,垂足为G,G在AD上,且![]() ,
,![]() ,
,![]() ,
,![]() ,E是BC的中点.
,E是BC的中点.
![]() 求异面直线GE与PC所成的角的余弦值;
求异面直线GE与PC所成的角的余弦值;
![]() 求点D到平面PBG的距离;
求点D到平面PBG的距离;
![]() 若F点是棱PC上一点,且
若F点是棱PC上一点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥V﹣ABCD中(底面是正方形,侧棱均相等),AB=2,VA= ![]() ,且该四棱锥可绕着AB任意旋转,旋转过程中CD∥平面α,则正四棱锥V﹣ABCD在平面α内的正投影的面积的取值范围是( )
,且该四棱锥可绕着AB任意旋转,旋转过程中CD∥平面α,则正四棱锥V﹣ABCD在平面α内的正投影的面积的取值范围是( )
A.[2,4]
B.(2,4]
C.[ ![]() ,4]
,4]
D.[2,2 ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(﹣2sin(π﹣x),cosx),
=(﹣2sin(π﹣x),cosx), ![]() =(
=( ![]() cosx,2sin(
cosx,2sin( ![]() ﹣x)),函数f(x)=1﹣
﹣x)),函数f(x)=1﹣ ![]()
![]() .
.
(1)若x∈[0, ![]() ],求函数f(x)的值域;
],求函数f(x)的值域;
(2)当x∈[0,π]时,求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是ρ=2,矩形ABCD内接于曲线C1 , A,B两点的极坐标分别为(2, ![]() )和(2,
)和(2, ![]() ),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
(1)写出C,D的直角坐标及曲线C2的参数方程;
(2)设M为C2上任意一点,求|MA|2+|MB|2+|MC|2+|MD|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣2sin2x+2 ![]() sinxcosx+1.
sinxcosx+1.
(1)求f(x)的最小正周期及对称中心;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值和最小值.
],求f(x)的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com