练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．对大于或等于2的自然数m的n次方幂有如下分解式：22=1+3，32=1+3+5，42=1+3+5+7；23=3+5，33=7+9+11，43=13+15+17+19．
    根据上述分解规律52=1+3+5+7+9，则53的分解中最大的数是29．

    分析 由由23=3+5，33=7+9+11，43=13+15+17+19，可得53=21+23+25+27+29，问题得以解决

    解答 解：由23=3+5，33=7+9+11，43=13+15+17+19，
    可得53=21+23+25+27+29，
    故53的分解中最大的数是29，
    故答案为29

    点评 本题考查归纳推理，求解的关键是根据归纳推理的原理归纳出结论，其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知E（2，2）是抛物线C：y2=2px上一点，经过点D（2，0）的直线l与抛物线C交于A，B两点（不同于点E），直线EA，EB分别交直线x=-2于点M，N
    （1）求抛物线方程及其焦点坐标，准线方程；
    （2）已知O为原点，求证：∠MON为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．角α的终边在第三象限，那么$\frac{α}{3}$的终边不可能在的象限是第（　　）象限．
    A．一B．二C．三D．四

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在Rt△ABC中，∠C=90°，AC=4，则$\overrightarrow{AB}$•$\overrightarrow{CA}$等于（　　）
    A．-16B．-8C．16D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．因为指数函数y=ax是增函数，而y=（$\frac{1}{2}$）x是指数函数，所以y=（$\frac{1}{2}$）x是增函数关于上面推理正确的说法是（　　）
    A．推理的形式错误B．大前提是错误的C．小前提是错误的D．结论是正确的

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

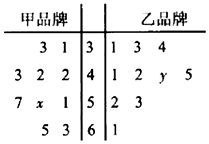    13．某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动，为调查这100天的日销售情况，用简单随机抽样抽取10天进行统计，以它们的销售数量（单位：件）作为样本，样本数据的茎叶图如图．已知该样本中，甲品牌牛奶销量的平均数为48件，乙品牌牛奶销量的中位数为43件，将日销量不低于50件的日期称为“畅销日”．
    （1）求出x，y的值；
    （2）以10天的销量为样本，估计100天的销量，请完成这两种品牌100天销量的2×2列联表，并判断是否有99%的把握认为品牌与“畅销日”天数相关．
    畅销日天数非畅销日天数合计
    甲5050100              
    乙3070100
    合计80120200
    附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$（其中n=a+b+c+d为样本容量）
    P（K2≥k0）0.0500.0100.001
    k03.8416.63510.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．独立性检验中，假设H0：变量X与变量Y没有关系，则在H0成立的情况下，P（K2≥6.635）≈0.010表示的意义是（　　）
    A．变量X与变量Y有关系的概率为1%
    B．变量X与变量Y有关系的概率为99.9%
    C．变量X与变量Y没有关系的概率为99%
    D．变量X与变量Y有关系的概率为99%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若椭圆$\frac{x^2}{36}+\frac{y^2}{16}=1$上一点P与椭圆的两个焦点F1、F2的连线互相垂直，则△PF1F2的面积为（　　）
    A．36B．16C．20D．24

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．某班级50名学生的考试分数x分布在区间[50，100）内，设考试分数x的分布频率是f（x），且$f（x）=\left\{\begin{array}{l}\frac{n}{10}-0.4，10n≤x＜10（{n+1}），n=5，6，7\\-\frac{n}{5}+b，10n≤x＜10（{n+1}），n=8，9.\end{array}\right.$
    （1）求b的值；
    （2）并估计班级的考试平均分数；
    （3）考试成绩采用“5分制”，规定：考试分数在[50，60）内的成绩记为1分，考试分数在[60，70）内的成绩记为2分，考试分数在[70，80）内的成绩记为3分，考试分数在[80，90）内的成绩记为4分，考试分数在[90，100）内的成绩记为5分，在50名学生中用分层抽样的方法，从成绩为1分，2分，3分的学生中随机抽取6人，再从这6人中抽出2人，记这2人的成绩之和为4的概率（将频率视为概率）．

    查看答案和解析>>

    同步练习册答案