
 A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.分析 (1)根据点A的坐标,得出sinα与cosα的值,代入计算即可;
(2)用α表示出∠BOC,再利用余弦定理写出|BC|2的表达式,求出它的取值范围即可.
解答 解:(1)∵A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),
∴sinα=$\frac{4}{5}$,cosα=$\frac{3}{5}$;
∴$\frac{2sinα•sinα}{co{s}^{2}α+1-2si{n}^{2}α}$=$\frac{2×\frac{4}{5}×\frac{3}{5}}{{(\frac{3}{5})}^{2}+1-2{×(\frac{4}{5})}^{2}}$=12;
(2)∵∠AOC=α,α∈(0,$\frac{π}{2}$),
∴∠BOC=α+$\frac{π}{2}$;
∴|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos∠BOC
=1+1-2cos(α+$\frac{π}{2}$)=2+2sinα,
又α∈(0,$\frac{π}{2}$),
∴sinα∈(0,1),
∴2+2sinα∈(2,4),
即|BC|2的取值范围是(2,4).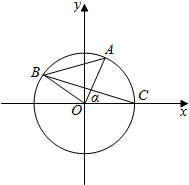
点评 本题考查了三角函数的定义与三角函数式的化简求值问题,也考查了余弦定理的应用问题,是基础题目.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:高中数学 来源: 题型:选择题
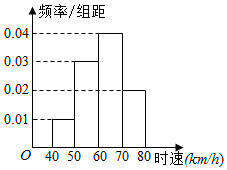 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>1 | B. | b>a>1 | C. | a>1,0<b<1 | D. | 0<a<1,b>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{43}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\sqrt{73}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | C${\;}_{100}^{3}$ | C. | -2C${\;}_{100}^{3}$ | D. | 2100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com