
分析 求函数的对数,利用复合函数的导数法则进行求解即可.
解答 解:(1)y=$\sqrt{\frac{x+1}{x-1}}$;
则lny=ln$\sqrt{\frac{x+1}{x-1}}$=$\frac{1}{2}$ln(x+1)-$\frac{1}{2}$ln(x-1);
则$\frac{1}{y}$•y′=$\frac{1}{2(x+1)}-\frac{1}{2(x-1)}$=-$\frac{1}{{x}^{2}-1}$,
则y′=-$\frac{1}{{x}^{2}-1}$•y=-$\frac{1}{{x}^{2}-1}$•$\sqrt{\frac{x+1}{x-1}}$;
(2)y=xx.
则lny=lnxx=xlnx,
则$\frac{1}{y}$•y′=lnx+x$•\frac{1}{x}$=lnx+1,
则y′=(lnx+1)y=(lnx+1)xx,
点评 本题主要考查函数的导数的计算,利用取对数法,结合复合函数的导数公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
 A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.
A、B是单位圆O上的动点,且A、B分别在第--象限,C是圆0与π轴正半轴的交点,△A0B为等腰直角三角形,记∠AOC=α.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
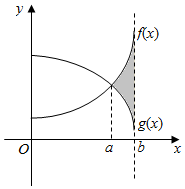 如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.
如图所示,已知${∫}_{0}^{b}$f(x)dx=11,${∫}_{0}^{b}$g(x)dx=9,${∫}_{0}^{a}$[g(x)-f(x)]dx=5.则图中阴影部分的面积为7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
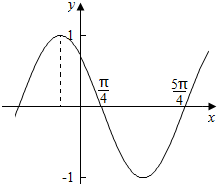
| A. | (kπ+$\frac{3}{4}$π,kπ+$\frac{7}{4}$π),k∈Z | B. | (kπ+$\frac{π}{4}$,kπ+$\frac{5π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{5}{4}$π),k∈Z | D. | (2k+$\frac{3}{4}$π,2k+$\frac{7}{4}$π),k∈Z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com