
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 由题意,f'(x)≥0恒成立,可求出关于a,c的不等式,联立ac≤4,化简$\frac{a}{{c}^{2}+4}$+$\frac{c}{{a}^{2}+4}$并求出其最小值.
解答 解:由题意,
因为函数f(x)=$\frac{1}{3}$ax3-2x2+cx在R上单调递增,
所以f'(x)=ax2-4x+c≥0恒成立,
所以$\left\{\begin{array}{l}{a>0}\\{△=16-4ac≤0}\end{array}\right.$,
所以ac≥4,
又因为ac≤4,
所以ac=4且a>0,c>0,
$\frac{a}{{c}^{2}+4}$+$\frac{c}{{a}^{2}+4}$=$\frac{a}{{c}^{2}+ac}+\frac{c}{{a}^{2}+ac}$=$\frac{a}{c(c+a)}+\frac{c}{a(c+a)}$
=$\frac{1}{c}-\frac{1}{c+a}+\frac{1}{a}-\frac{1}{c+a}$=($\frac{1}{a}+\frac{1}{c}$)-$\frac{2}{c+a}$≥$2\sqrt{\frac{1}{ac}}-\frac{2}{2\sqrt{ac}}$=1-$\frac{1}{2}$=$\frac{1}{2}$;
故选:C.
点评 本题考查了利用导数求函数单调性,基本不等式等内容,解题关键是将函数单调性问题转化为恒成立问题,以及观察式子将其转化为与已知条件相关的形式即转化为与ac=4相关的问题.难度属于中上档.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 25π | B. | 36π | C. | 49π | D. | 32π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [$\frac{1}{5}$,1] | C. | (1,+∞)∪(-∞,$\frac{1}{5}$) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+2y+5=0 | B. | 2x+y-5=0 | C. | x+2y-5=0 | D. | x-2y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
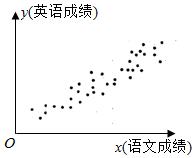 为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线$\hat y$=$\hat b$x+$\hat a$近似地刻画其相关系,根据图形,以下结论最有可能成立的是( )
为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线$\hat y$=$\hat b$x+$\hat a$近似地刻画其相关系,根据图形,以下结论最有可能成立的是( )| A. | 线性相关关系较强,b的值为3.25 | B. | 线性相关关系较强,b的值为0.83 | ||
| C. | 线性相关关系较强,b的值为-0.87 | D. | 线性相关关系太弱,无研究价值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\sqrt{5}$ | B. | ±$\sqrt{10}$ | C. | ±2$\sqrt{5}$ | D. | ±$\sqrt{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com