
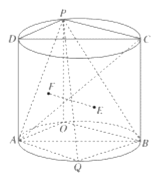
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点P是圆弧
是边长为2的正方形,点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点Q是圆弧
重合),点Q是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点P在平面![]() 上的射影为点O,点
上的射影为点O,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(i)证明:![]() 平面
平面![]() ;
;
(ii)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)(i)证明见解析(ii)![]()
【解析】
(1)由![]() ,
,![]() 可得
可得![]() 平面
平面![]() ,即可证明;
,即可证明;
(2)(i)连接![]() 并延长交
并延长交![]() 于点M,连接
于点M,连接![]() 并延长交
并延长交![]() 于点N,连接
于点N,连接![]() ,利用平行线分线段成比例可得
,利用平行线分线段成比例可得![]() ,即可得
,即可得![]() 得证;
得证;
(ii)根据![]() 即可求解.
即可求解.
(1)证明:因为![]() 是轴截面,
是轴截面,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
又点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),且
重合),且![]() 为直径,
为直径,
所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() .
.
(2)当三棱锥![]() 体积最大时,点P为圆弧
体积最大时,点P为圆弧![]() 的中点.所以点O为圆弧
的中点.所以点O为圆弧![]() 的中点,
的中点,
所以四边形![]() 为正方形,且
为正方形,且![]() 平面
平面![]() .
.
(i)证明:连接![]() 并延长交
并延长交![]() 于点M,连接
于点M,连接![]() 并延长交
并延长交![]() 于点N,连接
于点N,连接![]() ,
,
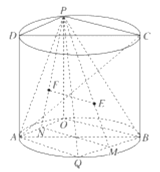
则![]() ,
,
因为![]() 分别为三角形的重心,所以
分别为三角形的重心,所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(ii)因为![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高.
的高.
又![]() ,
,![]() ,
,
所以![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数)
为参数)![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,试判断直线
,试判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,若点
,若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com