
【题目】在平面直角坐标中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数)
为参数)![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,试判断直线
,试判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,若点
,若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的面积.
的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
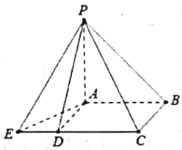
【题目】中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑,如图为一个阳马与一个鳖臑的组合体,已知![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,
,![]() ,若鳖臑
,若鳖臑![]() 的外接球的体积为
的外接球的体积为![]() ,则阳马
,则阳马![]() 的外接球的表面积等于______。
的外接球的表面积等于______。
查看答案和解析>>
科目:高中数学 来源: 题型:
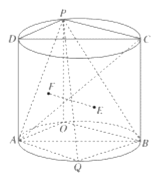
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点P是圆弧
是边长为2的正方形,点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点Q是圆弧
重合),点Q是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点P在平面![]() 上的射影为点O,点
上的射影为点O,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(i)证明:![]() 平面
平面![]() ;
;
(ii)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com