
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
(Ⅰ)若椭圆V过点(﹣ ![]() ,
, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(Ⅱ)若直线l:y=kx+b与椭圆C交于B、P两点,若以PQ为直径的圆过点B,证明:存在k∈R, ![]() =
= ![]() .
.
【答案】解:(Ⅰ)椭圆的离心率e= ![]() =
= ![]() =
= ![]() ,则a2=2b2 ,
,则a2=2b2 ,
将点(﹣ ![]() ,
, ![]() )代入椭圆方程
)代入椭圆方程 ![]() ,解得:a2=4,b2=2,
,解得:a2=4,b2=2,
∴椭圆的标准方程为: ![]() ,
,
(Ⅱ)由题意的对称性可知:设存在存在k>0,使得 ![]() =
= ![]() ,
,
由a2=2b2 , 椭圆方程为: ![]() ,
,
将直线方程代入椭圆方程,整理得:(1+2k2)x2+4kbx=0,
解得:xP=﹣ ![]() ,则丨BP丨=
,则丨BP丨= ![]() ×
× ![]() ,
,
由BP⊥BQ,则丨BQ丨= ![]() ×丨
×丨 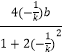 丨=
丨= ![]()
![]() ,
,
由 ![]() =
= ![]() .,则2
.,则2 ![]() ×
× ![]() =
= ![]()
![]() ,
,
整理得:2k3﹣2k2+4k﹣1=0,
设f(x)=2k3﹣2k2+4k﹣1,由f( ![]() )<0,f(
)<0,f( ![]() )>0,
)>0,
∴函数f(x)存在零点,
∴存在k∈R, ![]() =
= ![]()
【解析】(Ⅰ)由椭圆的离心率公式求得a和b的关系,将(﹣ ![]() ,
, ![]() )代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,求得P的横坐标,求得丨BP丨,利用直线垂直的斜率关系求得丨BQ丨,由
)代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)将直线方程代入椭圆方程,求得P的横坐标,求得丨BP丨,利用直线垂直的斜率关系求得丨BQ丨,由 ![]() =
= ![]() ,根据函数零点的判断即可存在k∈R,
,根据函数零点的判断即可存在k∈R, ![]() =
= ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某市电视台为了提高收视率而举办有奖问答活动,随机对该市15~65岁的人群抽样了 ![]() 人,回答问题统计结果及频率分布直方图如图表所示.
人,回答问题统计结果及频率分布直方图如图表所示.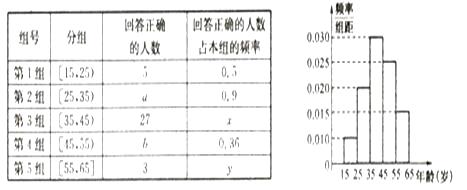
(1)分别求出 ![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]()
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设直线 ![]() 与圆
与圆 ![]() 相切于点
相切于点 ![]() ,且
,且 ![]() 与椭圆
与椭圆 ![]() 只有一个公共点
只有一个公共点 ![]() .
.
①求证: ![]() ;
;
②当 ![]() 为何值时,
为何值时, ![]() 取得最大值?并求出最大值.
取得最大值?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,其中a>0.
,其中a>0.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2).
(n∈N* , n≥2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(普通班)学校食堂定期从某粮店以每吨 ![]() 元的价格买大米,每次购进大米需支付运输劳务费
元的价格买大米,每次购进大米需支付运输劳务费 ![]() 元,已知食堂每天需要大米
元,已知食堂每天需要大米 ![]() 吨,贮存大米的费用为每吨每天
吨,贮存大米的费用为每吨每天 ![]() 元,假定食堂每次均在用完大米的当天购买.
元,假定食堂每次均在用完大米的当天购买.
(1)该食堂每多少天购买一次大米,能使平均每天所支付的费用最少?
(2)粮店提出价格优惠条件:一次购买量不少于 ![]() 吨时,大米价格可享受九五折优惠(即是原价的
吨时,大米价格可享受九五折优惠(即是原价的 ![]() ),问食堂可否接受此优惠条件?请说明理由.
),问食堂可否接受此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产不同规格的一种产品,根据检测标准,其合格产品的质量 ![]() 与尺寸
与尺寸 ![]() 之间满足关系式
之间满足关系式 ![]() 为大于
为大于 ![]() 的常数),现随机抽取6件合格产品,测得数据如下:
的常数),现随机抽取6件合格产品,测得数据如下:
对数据作了处理,相关统计量的值如下表:
(1)根据所给数据,求 ![]() 关于
关于 ![]() 的回归方程(提示:由已知,
的回归方程(提示:由已知, ![]() 是
是 ![]() 的线性关系);
的线性关系);
(2)按照某项指标测定,当产品质量与尺寸的比在区间 ![]() 内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
内时为优等品,现从抽取的6件合格产品再任选3件,求恰好取得两件优等品的概率;
(附:对于一组数据 ![]() ,其回归直线
,其回归直线 ![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似地看出两条平行的直线,江岸的一侧有![]() ,
, ![]() 两个蔬菜基地,江岸的另一侧点
两个蔬菜基地,江岸的另一侧点![]() 处有一个超市.已知
处有一个超市.已知![]() 、
、![]() 、
、![]() 中任意两点间的距离为
中任意两点间的距离为![]() 千米,超市欲在
千米,超市欲在![]() 之间建一个运输中转站
之间建一个运输中转站![]() ,
, ![]() ,
, ![]() 两处的蔬菜运抵
两处的蔬菜运抵![]() 处后,再统一经过货轮运抵
处后,再统一经过货轮运抵![]() 处,由于
处,由于![]() ,
, ![]() 两处蔬菜的差异,这两处的运输费用也不同.如果从
两处蔬菜的差异,这两处的运输费用也不同.如果从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元.从
元.从![]() 处出发的运输费为每千米
处出发的运输费为每千米![]() 元,货轮的运输费为每千米
元,货轮的运输费为每千米![]() 元.
元.

(1)设![]() ,试将运输总费用
,试将运输总费用![]() (单位:元)表示为
(单位:元)表示为![]() 的函数
的函数![]() ,并写出自变量的取值范围;
,并写出自变量的取值范围;
(2)问中转站![]() 建在何处时,运输总费用
建在何处时,运输总费用![]() 最小?并求出最小值.
最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com