练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆 的离心率为 ，且过点
    （Ⅰ）求椭圆 的方程；
    （Ⅱ）设直线 与圆 相切于点 ，且 与椭圆 只有一个公共点 .
    ①求证： ；
    ②当 为何值时， 取得最大值？并求出最大值.

    【答案】解：(I)椭圆E的方程为
    （Ⅱ）①因为直线 与圆C: 相切于A,得 ,
    即 ①
    又因为 与椭圆E只有一个公共点B ，
    由 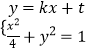得 ,且此方程有唯一解.
    则 即
    ②由①②,得
    ②设 ，由 得
    由韦达定理,
    ∵ 点在椭圆上,∴
    ∴
    在直角三角形OAB中,

    ∴
    【解析】（1）根据椭圆的性质得到，，再将点（，2）代入椭圆方程，解方程组即可得到。
    （2）①根据直线与圆的位置关系，利用点到直线的距离公式可以得到t，k，R的等量关系；再根据直线与椭圆的交点为一个，联立方程，可得=0；结合两个等式，消去t2即可得到。
    ②因为是直角三角形，故根据勾股定理可得,而OA长为R，故要将B点坐标用R表示出来，代入等式即可得到AB的长度。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】潮州统计局就某地居民的月收入调查了人，并根据所得数据画了样本的频率分

    布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在）。

    （1）求居民月收入在的频率；

    （2）根据频率分布直方图算出样本数据的中位数；

    （3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这人中分层抽样方法抽出人作进一步分析，则月收入在的这段应抽多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A,B,C所对的边分别为a,b,c，已知A为钝角，且2a ，若 ，则△ABC的面积的最大值为 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在△ABC中，角A，B，C所对的边分别是a，b，c，且a、b、c成等比数列，c= bsinC﹣ccosB．
    （Ⅰ）求B的大小；
    （Ⅱ）若b=2 ，求△ABC的周长和面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知以点为圆心的圆过点和，线段的垂直平分线交圆于点、，且,

    （1）求直线的方程； （2）求圆的方程。

    （3）设点在圆上，试探究使的面积为 8 的点共有几个？证明你的结论

    查看答案和解析>>

    科目：高中数学 来源： 题型：

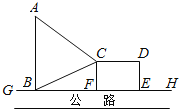
    【题目】如图，是东西方向的公路北侧的边缘线，某公司准备在上的一点的正北方向的处建一仓库，并在公路同侧建造一个正方形无顶中转站（其中边在上），现从仓库向和中转站分别修两条道路，，已知，且，设，．

    （1）求关于的函数解析式；

    （2）如果中转站四周围墙（即正方形周长）造价为万元，两条道路造价为万元，问：取何值时，该公司建中转围墙和两条道路总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： + =1（a＞b＞0）的离心率为 ，点B是椭圆C的上顶点，点Q在椭圆C上（异于B点）．
    （Ⅰ）若椭圆V过点（﹣ ， ），求椭圆C的方程；
    （Ⅱ）若直线l：y=kx+b与椭圆C交于B、P两点，若以PQ为直径的圆过点B，证明：存在k∈R， = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是我国古代内容极为丰富的数学名著，书中提到了一种名为“刍甍”的五面体（如图）面 为矩形，棱 .若此几何体中， ， 和 都是边长为 的等边三角形，则此几何体的表面积为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的离心率为 ，且过点 .
    （1）求椭圆 的方程；
    （2）设不过原点 的直线 与椭圆 交于 两点，直线 的斜率分别为 ，满足 ，试问：当 变化时， 是否为定值？若是，求出此定值，并证明你的结论；若不是，请说明理由.

    查看答案和解析>>

    同步练习册答案