
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,其中a>0.
,其中a>0.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2).
(n∈N* , n≥2).
【答案】解:(Ⅰ)函数f(x)的定义域是(0,+∞), f′(x)= ![]() ,令h(x)=﹣ax2+x﹣a,
,令h(x)=﹣ax2+x﹣a,
记△=1﹣4a2 , 当△≤0时,得a≥ ![]() ,
,
若a≥ ![]() ,则﹣ax2+x﹣a≤0,f′(x)≤0,
,则﹣ax2+x﹣a≤0,f′(x)≤0,
此时函数f(x)在(0,+∞)递减,
当0<a< ![]() 时,由﹣ax2+x﹣a=0,解得:x1=
时,由﹣ax2+x﹣a=0,解得:x1= ![]() ,x2=
,x2= ![]() ,
,
显然x1>x2>0,故此时函数f(x)在( ![]() ,
, ![]() )递增,
)递增,
在(0, ![]() )和(
)和( ![]() ,+∞)递减;
,+∞)递减;
综上,0<a< ![]() 时,函数f(x)在(
时,函数f(x)在( ![]() ,
, ![]() )递增,
)递增,
在(0, ![]() )和(
)和( ![]() ,+∞)递减,
,+∞)递减,
a≥ ![]() 时,函数f(x)在(0,+∞)递减;
时,函数f(x)在(0,+∞)递减;
(Ⅱ)证明:令a= ![]() ,由(Ⅰ)中讨论可得函数f(x)在区间(0,+∞)递减,
,由(Ⅰ)中讨论可得函数f(x)在区间(0,+∞)递减,
又f(1)=0,从而当x∈(1,+∞)时,有f(x)<0,即lnx< ![]() x﹣
x﹣ ![]() ,
,
令x=1+ ![]() (n≥2),
(n≥2),
则ln(1+ ![]() )<
)< ![]() (1+
(1+ ![]() )﹣
)﹣ 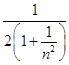 =
= 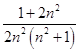
= ![]() (
( ![]() +
+ ![]() )<
)< ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
从而:ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+…+ln(1+
)+…+ln(1+ ![]() )
)
< ![]() (1﹣
(1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() )
)
= ![]() (1+
(1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )<
)< ![]() (1+
(1+ ![]() )=
)= ![]() ,
,
则有ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+ln(1+
)+ln(1+ ![]() )+…+ln(1+
)+…+ln(1+ ![]() )<
)< ![]() ,
,
可得(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2)
(n∈N* , n≥2)
【解析】(Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅱ)求出lnx< ![]() x﹣
x﹣ ![]() ,令x=1+
,令x=1+ ![]() (n≥2),得到ln(1+
(n≥2),得到ln(1+ ![]() )<
)< ![]() (
( ![]() ﹣
﹣ ![]() ),累加即可证明结论.
),累加即可证明结论.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.![]() ,y
,y ![]() R,若x+y
R,若x+y ![]() 0,则x
0,则x ![]() 且y
且y ![]()
B.a ![]() R,“
R,“ ![]() ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“ ![]() x
x ![]() R,使得
R,使得 ![]() ”的否定是“
”的否定是“ ![]() R,都有
R,都有 ![]() ”
”
D.“若 ![]() ,则a<b”的逆命题为真命题
,则a<b”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C所对的边分别是a,b,c,且a、b、c成等比数列,c= ![]() bsinC﹣ccosB.
bsinC﹣ccosB.
(Ⅰ)求B的大小;
(Ⅱ)若b=2 ![]() ,求△ABC的周长和面积.
,求△ABC的周长和面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
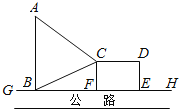
【题目】如图,![]() 是东西方向的公路北侧的边缘线,某公司准备在
是东西方向的公路北侧的边缘线,某公司准备在![]() 上的一点
上的一点![]() 的正北方向的
的正北方向的![]() 处建一仓库,并在公路同侧建造一个正方形无顶中转站
处建一仓库,并在公路同侧建造一个正方形无顶中转站![]() (其中边
(其中边![]() 在
在![]() 上),现从仓库
上),现从仓库![]() 向
向![]() 和中转站分别修两条道路
和中转站分别修两条道路![]() ,
,![]() ,已知
,已知![]() ,且
,且![]() ,设
,设![]() ,
,![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果中转站四周围墙(即正方形周长)造价为![]() 万元
万元![]() ,两条道路造价为
,两条道路造价为![]() 万元
万元![]() ,问:
,问:![]() 取何值时,该公司建中转围墙和两条道路总造价
取何值时,该公司建中转围墙和两条道路总造价![]() 最低?
最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
,点B是椭圆C的上顶点,点Q在椭圆C上(异于B点).
(Ⅰ)若椭圆V过点(﹣ ![]() ,
, ![]() ),求椭圆C的方程;
),求椭圆C的方程;
(Ⅱ)若直线l:y=kx+b与椭圆C交于B、P两点,若以PQ为直径的圆过点B,证明:存在k∈R, ![]() =
= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图)面 ![]() 为矩形,棱
为矩形,棱 ![]() .若此几何体中,
.若此几何体中, ![]() ,
, ![]() 和
和 ![]() 都是边长为
都是边长为 ![]() 的等边三角形,则此几何体的表面积为( )
的等边三角形,则此几何体的表面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x﹣4|.
(Ⅰ)记函数g(x)=f(x)+|x+2|﹣4,在下列坐标系中作出函数g(x)的图象,并根据图象求出函数g(x)的最小值;
(Ⅱ)记不等式f(x)<5的解集为M,若p,q∈M,且|p+q+pq|<λ,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com