
【题目】如图,在三棱锥![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.已知
的中点.已知![]() ,
,![]() .
.

求证:(1)直线PA![]() 平面DEF;
平面DEF;
(2)平面BDE⊥平面ABC.
【答案】(1)见解析(2)见解析
【解析】
试题分析:(1) 由线面平行的判定定理可知,只须证PA与平面DEF内的某一条直线平行即可,由已知及图形可知应选择DE,由三角形的中位线的性质易知: DE∥PA ,从而问题得证;注意线PA在平面DEG外,而DE在平面DEF内必须写清楚;(2) 由面面垂直的判定定理可知,只须证两平中的某一直线与另一个平面垂直即可,注意题中已知了线段的长度,那就要注意利用勾股定理的逆定理来证明直线与直线的垂直;通过观察可知:应选择证DE垂直平面ABC较好,由(1)可知:DE⊥AC,再就只须证DE⊥EF即可;这样就能得到DE⊥平面ABC,又DE![]() 平面BDE,从面而有平面BDE⊥平面ABC.
平面BDE,从面而有平面BDE⊥平面ABC.
试题解析:(1)因为D,E分别为PC,AC的中点,所以DE∥PA.
又因为PA![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,所以直线PA∥平面DEF.
平面DEF,所以直线PA∥平面DEF.
(2)因为D,E,F分别人棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=![]() PA=3,EF=
PA=3,EF=![]() BC=4.
BC=4.
又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90。,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC![]() 平面ABC,EF
平面ABC,EF![]() 平面ABC,所以DE⊥平面ABC.
平面ABC,所以DE⊥平面ABC.
又DE![]() 平面BDE,所以平面BDE⊥平面ABC.
平面BDE,所以平面BDE⊥平面ABC.


科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
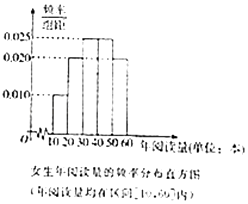
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
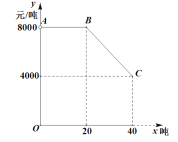
【题目】乔经理到老陈的果园里一次性采购一种水果,他俩商定:乔经理的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间函数关系的图像如图中的折线段
(吨)之间函数关系的图像如图中的折线段![]() 所示(不包含端点
所示(不包含端点![]() 但包含端点
但包含端点![]() ).
).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)已知老陈种植水果的成本是2800元/吨,那么乔经理的采购量为多少时,老陈在这次买卖中所获的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,其中a>0.
,其中a>0.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2).
(n∈N* , n≥2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.如果平面 ![]() 平面
平面 ![]() ,则
,则 ![]() 内任意一条直线必垂直于
内任意一条直线必垂直于 ![]()
B.若直线 ![]() 不平行于平面
不平行于平面 ![]() ,则
,则 ![]() 内不存在直线平行于直线
内不存在直线平行于直线 ![]()
C.如果平面 ![]() 不垂直于平面
不垂直于平面 ![]() ,那么平面
,那么平面 ![]() 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 ![]()
D.若直线 ![]() 不垂直于平面
不垂直于平面 ![]() ,则
,则 ![]() 内不存在直线垂直于直线
内不存在直线垂直于直线 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,曲线C1的参数方程为 ![]() (φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(φ为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2cosθ.
(Ⅰ)求曲线C1的极坐标方程与曲线C2的直角坐标方程;
(Ⅱ)若直线θ= ![]() (ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
(ρ∈R)与曲线C1交于P,Q两点,求|PQ|的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆命题为“若
”的逆命题为“若 ![]() ,则
,则 ![]() ”
”
B.对于命题 ![]() ,使得
,使得 ![]() ,则
,则 ![]() ,则
,则 ![]()
C.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
D.若 ![]() 为假命题,则
为假命题,则 ![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知圆
中,已知圆 ![]() ,点
,点 ![]() ,点
,点 ![]() ,以B为圆心,
,以B为圆心, ![]() 为半径作圆,交圆C于点P,且
为半径作圆,交圆C于点P,且 ![]() 的平分线交线段CP于点Q.
的平分线交线段CP于点Q.
(1)当a变化时,点Q始终在某圆锥曲线 ![]() 上运动,求曲线
上运动,求曲线 ![]() 的方程;
的方程;
(2)已知直线l过点C,且与曲线 ![]() 交于M,N两点,记
交于M,N两点,记 ![]() 面积为
面积为 ![]() ,
, ![]() 面积为
面积为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com