
【题目】定义在R上的函数f(x)的图象关于y轴对称,且f(x)在[0,+∞)上单调递减,若关于x的不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)在x∈[1,3]上恒成立,则实数m的取值范围为( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
【答案】D
【解析】解:∴定义在R上的函数f(x)的图象关于y轴对称, ∴函数f(x)为偶函数,
∵函数数f(x)在[0,+∞)上递减,
∴f(x)在(﹣∞,0)上单调递增,
若不等式f(2mx﹣lnx﹣3)≥2f(3)﹣f(﹣2mx+lnx+3)对x∈[1,3]恒成立,
即f(2mx﹣lnx﹣3)≥f(3)对x∈[1,3]恒成立.
∴﹣3≤2mx﹣lnx﹣3≤3对x∈[1,3]恒成立,
即0≤2mx﹣lnx≤6对x∈[1,3]恒成立,
即2m≥ ![]() 且2m≤
且2m≤ ![]() 对x∈[1,3]恒成立.
对x∈[1,3]恒成立.
令g(x)= ![]() ,则 g′(x)=
,则 g′(x)= ![]() ,在[1,e)上递增,(e,3]上递减,∴g(x)max=
,在[1,e)上递增,(e,3]上递减,∴g(x)max= ![]() .
.
令h(x)= ![]() ,h′(x)=
,h′(x)= ![]() <0,在[1,3]上递减,∴h(x)min=
<0,在[1,3]上递减,∴h(x)min= ![]() .
.
综上所述,m∈[ ![]() ,
, ![]() ].
].
故选D.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知圆 ![]() :
: ![]() (其中
(其中 ![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)若点 ![]() 为曲线
为曲线 ![]() 上一点,过点
上一点,过点 ![]() 作曲线
作曲线 ![]() 的切线交圆
的切线交圆 ![]() 于不同的两点
于不同的两点 ![]() (其中
(其中 ![]() 在
在 ![]() 的右侧),已知点
的右侧),已知点 ![]() .求四边形
.求四边形 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有 2个红球和 2个白球的口袋中任取 2个球,则下列每对事件中,互斥事件的对数是( )对
(1)“至少有 1个白球”与“都是白球” (2)“至少有 1个白球”与“至少有 1个红球”
(3)“至少有 1个白球”与“恰有 2个白球” (4)“至少有 1个白球”与“都是红球”
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.![]() ,y
,y ![]() R,若x+y
R,若x+y ![]() 0,则x
0,则x ![]() 且y
且y ![]()
B.a ![]() R,“
R,“ ![]() ”是“a>1”的必要不充分条件
”是“a>1”的必要不充分条件
C.命题“ ![]() x
x ![]() R,使得
R,使得 ![]() ”的否定是“
”的否定是“ ![]() R,都有
R,都有 ![]() ”
”
D.“若 ![]() ,则a<b”的逆命题为真命题
,则a<b”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设公差大于0的等差数列{ ![]() }的前n项和为
}的前n项和为 ![]() .已知
.已知 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() 成等比数列.记数列
成等比数列.记数列 ![]() 的前n项和为
的前n项和为 ![]() .
.
(1)求 ![]() ;
;
(2)若对于任意的n ![]() ,k
,k ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA= ![]() ,PB=
,PB= ![]() ,则三棱锥P﹣ABC的外接球的表面积为 .
,则三棱锥P﹣ABC的外接球的表面积为 . 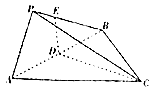
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com